控制流平坦化(control flow flattening)是作用于控制流图的代码混淆技术
其基本思想是重新组织函数的控制流图中的基本块关系,通过插入一个 “主分发器” 来控制基本块的执行流程
简而言之,就是基于 基本块,将 if else 跳转改成 switch case
平坦化前(竖向)
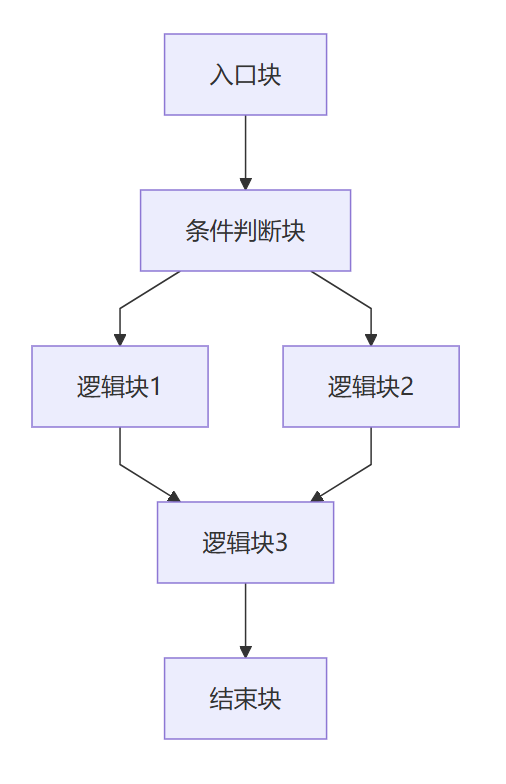
平坦化后(竖向)
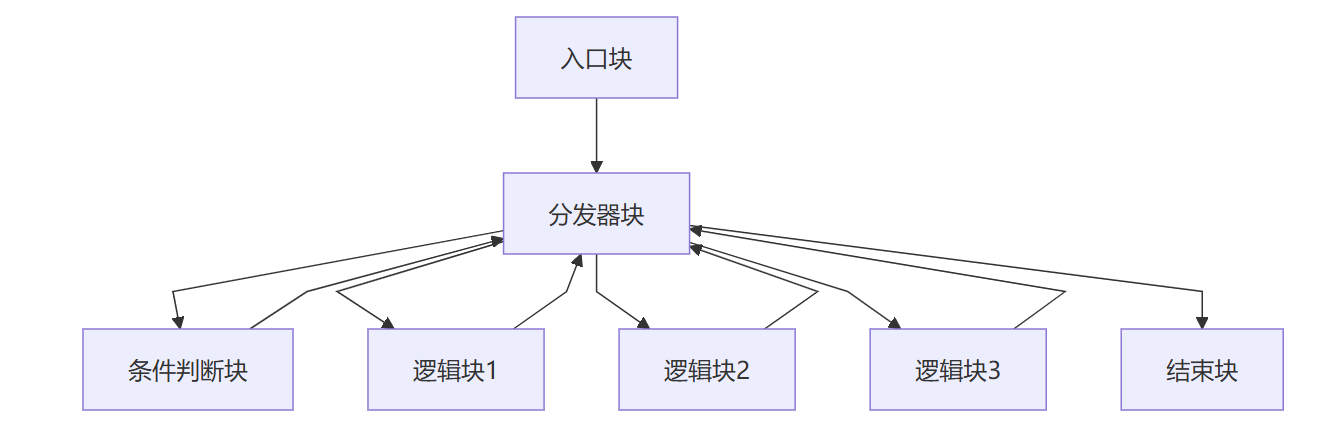
平坦化前(横向)
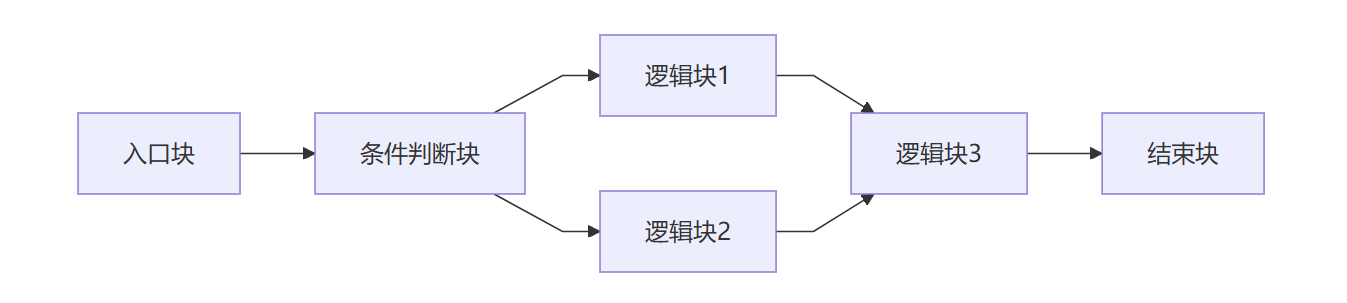
平坦化后(横向)
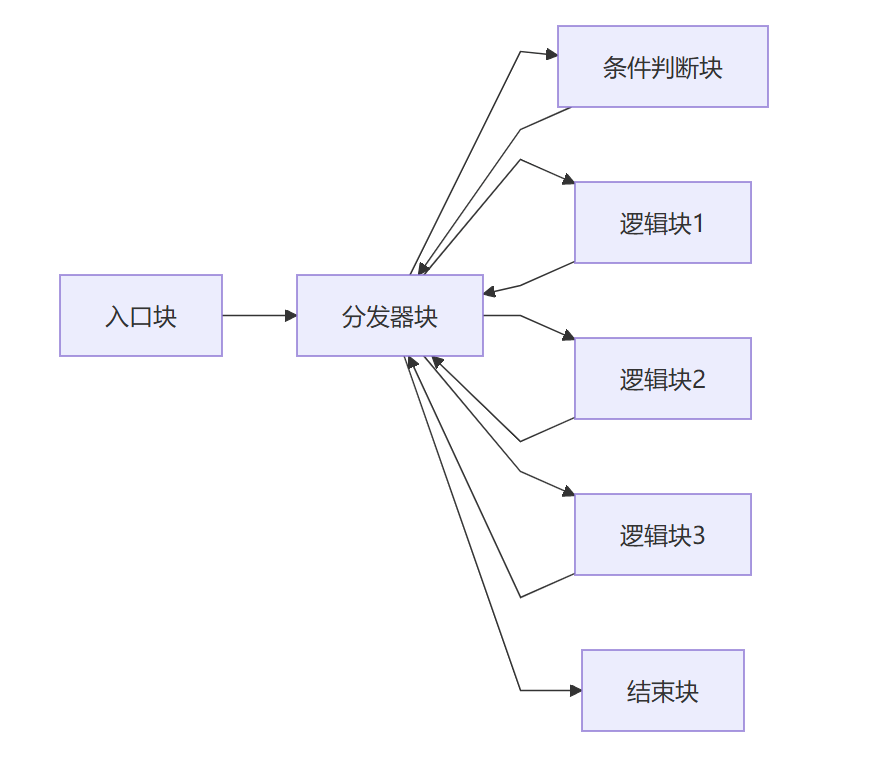
识别
控制流平坦化(Control Flow Flattening)是一种常见的混淆技术,它会导致 IDA 反编译器将原本结构化的控制流识别为一个大的 while 循环
IDA 反编译器看到这种结构时,会将其识别为一个无限循环(while (1)),因为:
平坦化前
void __fastcall sub_7C74C4(void **a1)
{
void *v1; // [xsp+8h] [xbp-8h]
v1 = *a1;
*a1 = 0LL;
if ( v1 )
sub_584190(v1);
}
平坦化后
void __fastcall sub_7C74C4(void **a1)
{
int v1; // w8
int v2; // w26
int i; // w8
void *v4; // [xsp+8h] [xbp-8h]
v4 = *a1;
*a1 = 0LL;
v1 = -877419764;
while ( v1 != -2045315170 )
{
if ( v1 == 1787132795 )
{
if ( v4 )
v2 = -1592215583;
else
v2 = 297951760;
for ( i = 1271350888; ; i = 297951760 )
{
while ( i == 1271350888 )
i = v2;
if ( i == 297951760 )
break;
sub_184190(v4);
}
v1 = -2045315170;
}
else if ( v4 )
{
v1 = 1787132795;
}
else
{
v1 = -2045315170;
}
}
}
反平坦化
基本概念
反平坦化需要引入几个基本的概念:
基本块
在 IDA 中,一个基本块(Basic Block)最多可以有两个后继,这是因为基本块的定义和控制流结构决定了它的后继数量通常不会超过两个。
原因如下:
[ol]
[/ol]
基本块之间的连接方式
基本块之间的连接主要通过以下方式实现:
[ol]
[/ol]
分发器
分发器 dispatcher 通常也可以被称作循环头 loophead
在控制流平坦化中,分发器通常具有以下特征:
[ol]
[/ol]
因此,识别循环头是识别分发器的一个有效策略,尤其在平坦化结构中,分发器往往就是那个“被回跳最多”的块
注意!!!!!!!!!!!!!!!!!!!
循环头并不一定是分发器
分发器根据状态变量的值引导程序执行真实的基本块。控制流平坦化中,分发器可能有一个或多个
状态变量
状态变量用于串联代码的真实代码块之间的逻辑关系,分发器根据状态变量的值选择执行对应的真实代码块,真实代码块执行后,需要更新状态变量以衔接下一个要执行的真实代码块
相当于 switch(状态变量) case
真实块
原始的基本块
函数入口
平坦化的最小单位是函数,与之对应,反平坦化的最小单位也是一个函数
函数入口就是这个函数的起始地址
核心
反平坦化的核心在于去掉分发器,修复每个真实块的后继
真实块也是基本块,因此至多只有 2 个后继,但前驱无上限(可以回顾前面的基本块定义)
所以修复真实块的关系核心是在找到真实块的后继上
对于每一个真实块,确定它的后继就能实现反平坦化了
以前面后继最多的条件判断块为例
平坦化前
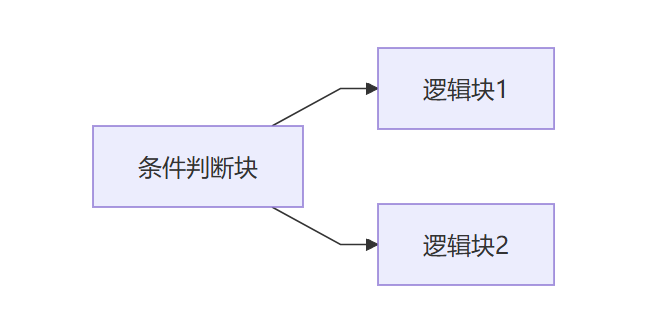
平坦化后
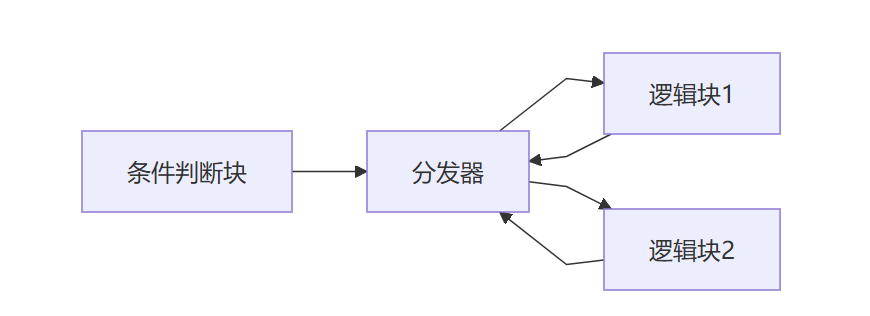
查找后继
于是问题被转换为了 :给定一个真实块的地址,确定该真实块的后继
这里就需要模拟执行了,从给定的真实块地址开始模拟执行,执行直到遇到其它真实块
需要进行 2 次模拟执行:
模拟执行的结果会有 3 种,对下面这 3 种情况有疑惑的可以结合前面 基本块之间的连接方式 来看
现在大致清楚模拟执行需要的参数和返回值了
但这里需要注意,直接从给定的真实块地址开始模拟执行会有一个问题,缺少对应的上下文环境
如果从函数入口(平坦化的基本单位是函数)到真实块地址之间包含部分初始化的代码(比如对寄存器赋值,然后后面的代码要用到对应的寄存器),就会导致模拟执行出错
确定上下文
于是问题又被转换为了:给定一个真实块的地址,确定从函数地址到该真实块地址的上下文环境
直接上案例:
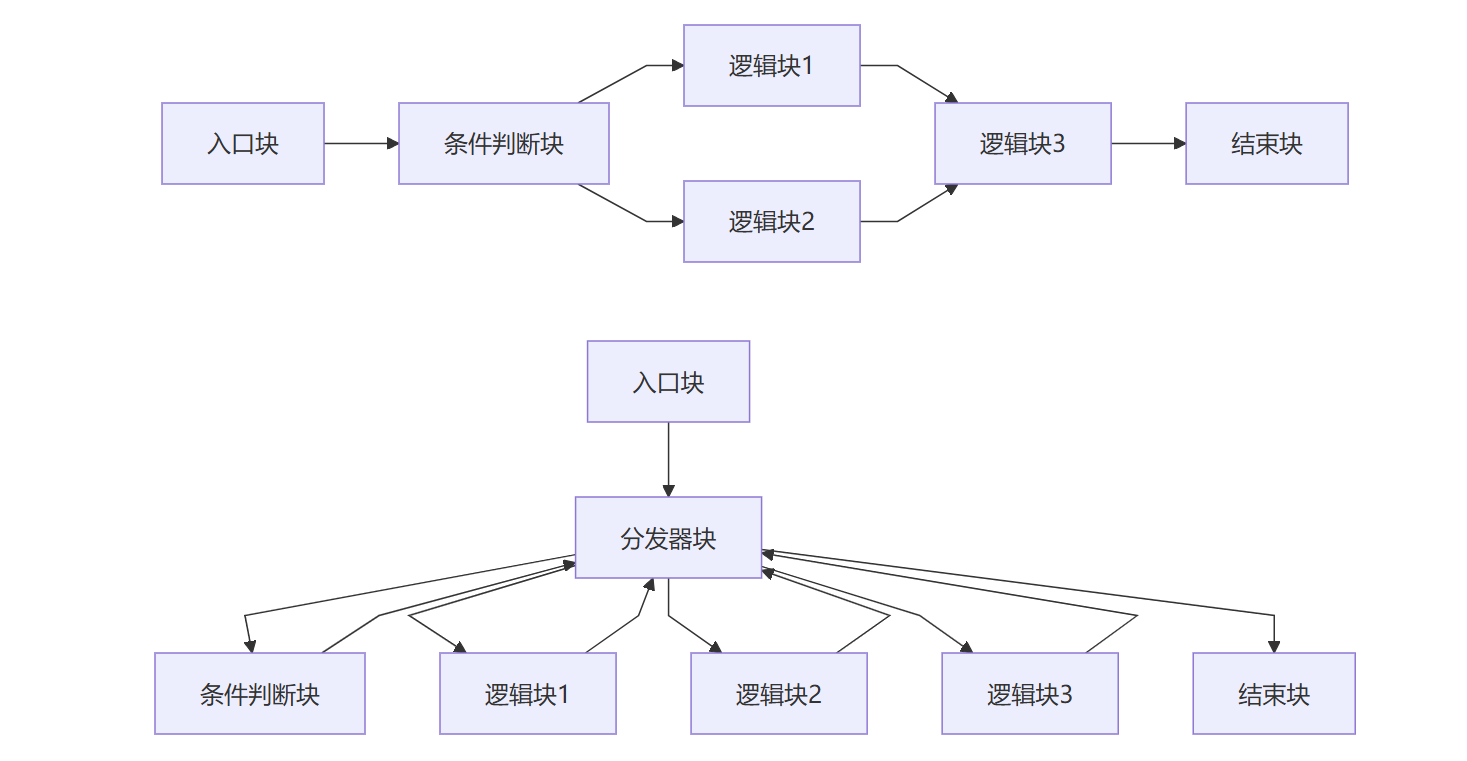
对于上面平坦化前后的函数,假如想要确定逻辑块3 的上下文,则需要确定从函数入口到逻辑块 3 的路径
这个路径被称为 : 关键路径
对于逻辑块3,它的关键路径是:
入口块 → 分发器块 → 条件判断块 → 分发器块 → 逻辑块1 → 分发器块 → 逻辑块3
或
入口块 → 分发器块 → 条件判断块 → 分发器块 → 逻辑块2 → 分发器块 → 逻辑块3
可以发现关键路径可能有多个,只要取任意一个即可
有了关键路径,只要沿着关键路径一路执行下来,就可以得到真实块对应的上下文了
再举个例子,对于结束块,它的关键路径是:
入口块 → 分发器块 → 条件判断块 → 分发器块 → 逻辑块1 → 分发器块 → 逻辑块3 → 分发器块 → 结束块
或
入口块 → 分发器块 → 条件判断块 → 分发器块 → 逻辑块1 → 分发器块 → 逻辑块3 → 分发器块 → 结束块
一般情况下:
但也有例外:
在一般情况下(真实块不依赖其它真实块的逻辑,或者哪怕依赖也不影响模拟执行),可以直接模拟执行到分发器后直接强制指定执行地址为真实块继续模拟执行
这样能够将模拟执行的基本单位从真实块扩大为分发器,大大提升模拟执行的效率
对于前面真实块,不难发现:条件判断块,逻辑块1,逻辑块2,逻辑块3,结束块,它们的分发器都是同一个分发器块
如果以真实块为基本单位,则需要模拟执行 5 次来确定上下文
但以分发器为基本单位,则只需要模拟执行 1 次就可以确定上下文
以分发器为基本单位,确定真实块的上下文就变成:给定一个真实块,查找该真实块的分发器,然后获取从函数入口执行到分发器的上下文即可
流程为:真实块 → 分发器 → 分发器的关键路径 → 分发器的上下文
对于前面的案例就是,如果想要确定逻辑块3 的上下文
流程就是:逻辑块3 → 分发器块 → (入口块 → 分发器块) → 分发器块的上下文
查找真实块对应分发器
给定一个真实块的地址,如何确定该真实块的分发器?
从 真实块地址 开始,向前遍历其前驱基本块,寻找是否有一个基本块在 所有分发器的 集合中。如果找到了,就返回该分发器块的地址
从 real_bb 开始,使用广度优先搜索(BFS)向前遍历其所有前驱基本块。
每次访问一个基本块地址 cur_ea:
def ida_get_bb(ea):
f_blocks = idaapi.FlowChart(idaapi.get_func(ea), flags=idaapi.FC_PREDS)
for block in f_blocks:
if block.start_ea
查找所有分发器
在前面分发器的基本概念中,有提到 :分发器 dispatcher 通常也可以被称作循环头 loophead
因此可以简单地以查找循环头来替代分发器的查找
使用深度优先搜索(DFS)从入口块开始遍历
如果某个块已经在当前路径中访问过,说明存在循环:
增加该块的访问计数。
如果访问次数达到或超过 min_loop_count,将其加入 loop_heads。
每次递归时复制 visited 集合,确保路径独立。
# 查找循环头
def find_loop_heads(func_entry, min_loop_count=1):
loop_heads = set()
loop_counter = defaultdict(int)
def dfs(block, visited):
if block.start_ea in visited:
loop_counter[block.start_ea] += 1
if loop_counter[block.start_ea] >= min_loop_count:
loop_heads.add(block.start_ea)
return
visited.add(block.start_ea)
for succ in block.succs():
dfs(succ, visited.copy())
entry_block = ida_get_bb(func_entry)
dfs(entry_block, set())
return list(loop_heads)
# 查找分发器
def find_dispachers(func):
# 通常循环头就是分发器
return find_loop_heads(func, 1)
查找关键路径
利用深度优先搜索在控制流图中查找从起始基本块到目标基本块的一条路径,并返回路径上的所有基本块地址范围
使用递归方式进行 DFS 遍历
visited 集合用于避免重复访问
path 列表记录当前路径上的基本块地址
DFS 逻辑:
# 查找关键路径
def find_key_path(start_bb_addr, end_bb_addr):
start_bb = ida_get_bb(start_bb_addr)
end_bb = ida_get_bb(end_bb_addr)
visited = set()
path = []
def dfs(cur_block):
if cur_block.start_ea in visited:
return False
visited.add(cur_block.start_ea)
path.append(cur_block.start_ea)
if cur_block.start_ea == end_bb.start_ea:
return True
for succ in cur_block.succs():
if dfs(succ):
return True
path.pop()
return False
if dfs(start_bb):
path = [ida_get_bb(b) for b in path]
path = [(b.start_ea, b.end_ea) for b in path]
return path
else:
return None
分发器块上下文
这一步需要进行模拟执行,具体逻辑和对应的模拟执行框架有关,比如常用的 angr, unicorn 等
因此只给出具体的思路,从函数入口开始,沿着关键路径执行到结束,最后返回结束时的上下文状态
查找所有真实块
真实块 通常指的是:
[ol]
[/ol]
这里的条件跳转指令又和对应的 架构 有关系了
以 arm64 为例,通常来说
B.EQ / TBNZ / CBZ
B.NE
会发现对于不同的条件跳转,需要进一步确定真实块是跳转地址还是不跳转地址,这个需要观察 IDA 的控制流图来具体确定
因此真实块的识别对于不同的案例并不一定能完全适用,需要具体情况具体分析,手动确定真实块以后,再去看对应的条件跳转判定
小结
结合前面的所有流程,可以总结出反平坦化的流程
def de_cff(func_entry):
# 根据分发器索引对应的上下文环境,避免反复模拟执行来获取分发器上下文
context_states = {}
# IDA 获取函数控制流图后,遍历所有基本块识别条件跳转,根据条件跳转的特点,确定跳转还是不跳转时对应的是真实块
# 需要具体情况具体分析,因此未提供代码
real_bbs = get_all_real_basic_blocks(func_entry)
# 查找所有分发器,通常可以直接用查找循环头来替代
# 从函数入口开始使用 DFS 遍历查找形成回环的基本块
dispachers = find_dispachers(func)
# 遍历所有真实块
for real_bb in real_bbs:
# 从真实块开始用 BFS 向前驱遍历查找分发器
dispacher = get_real_bb_dispatcher(real_bb, dispachers)
if dispatcher is None:
continue
# 如果还没有该分发器对应的上下文环境,则进行获取
if dispatcher not in context_states.keys():
# 使用 DFS 从函数入口开始查找分发器对应的关键路径
key_path = find_key_path(func_entry, dispatcher)
# 模拟执行获取分发器上下文,从函数入口沿关键路径执行返回执行结束的上下文状态
# 这里需要根据不同的模拟执行框架进行处理,因此未提供代码
context_state = simu_exec_path(key_path)
# 保存分发器上下文
context_states[dispatcher] = context_state
# 设置上下文下一次执行从真实块开始
set_pc(context_state, real_bb)
# 模拟执行 True, 从分发器上下文和真实块地址开始执行,中间遇到条件跳转一律改为强制跳转,直到遇见其它真实块才停止
succ_state1 = simu_run(context_state, True, real_bbs)
# 模拟执行 False, 从分发器上下文和真实块地址开始执行,中间遇到条件跳转一律改为不跳转,直到遇见其它真实块才停止
succ_state2 = simu_run(context_state, False, real_bbs)
修补
前面通过模拟执行,可以得到任意一个真实块模拟执行到其它真实块的状态
反平坦化的核心在于确定真实块的后继,要修补自然就是让真实块跳过分发器,"直达" 其它真实块
所谓的 "直达" 就是修改真实块的执行逻辑,让它 跳转 到其它真实块
要进行跳转,就绕不开 3 个问题
跳转起点
根据前面的分析可以知道,真实块和真实块之间的桥梁是分发器
修补要做的就是跳过分发器,因此可以将原本跳转到分发器的逻辑直接作为跳转的起点
通常来说真实块的结尾那部分逻辑可以直接作为跳转起点
需要注意的点就是,不要破坏原有的真实块的真实逻辑(非平坦化引入的混淆代码)
跳转目标
跳转目标自然就是其它真实块
跳转条件
在前面反平坦化的核心里有提到,模拟执行的结果可能有 3 个,这 3 个结果分别对应 3 种跳转条件
执行结果相同,且都是相同的真实块
直接跳转到这一个真实块即可
执行结果不同,但是不同的真实块
需要根据 True 和 False 时的条件,跳转到对应的真实块
执行结果没有找到真实块
没有跳转
修补参数
结合前面的分析,可以得到修补所需的内容
[table]
[tr]
[td][/td]
[td]说明[/td]
[/tr]
[tr]
[td]跳转起点

