概述
排序的复杂度一览
[td]算法[/td]
[td]时间复杂度:最好[/td]
[td]时间复杂度:平均[/td]
[td]时间复杂度:最坏[/td]
[td]空间复杂度:最坏[/td]
[td]稳定性[/td]
冒泡排序
O(n)
O(n^2)
O(n^2)
O(1)
稳定
选择排序
O(n^2)
O(n^2)
O(n^2)
O(1)
不稳定
插入排序
O(n)
O(n^2)
O(n^2)
O(1)
稳定
希尔排序
O(n)
O(n^3/2)
O(n^2)
O(1)
不稳定
快速排序
O(nlogn)
O(nlogn)
O(n^2)
O(logn)
不稳定
归并排序
O(nlogn)
O(nlogn)
O(nlogn)
O(n)
稳定
计数排序
O(n+k)
O(n+k)
O(n+k)
O(k)
稳定
基数排序
O(nk)
O(nk)
O(nk)
O(n+k)
稳定
堆排序
O(nlogn)
O(nlogn)
O(nlogn)
O(1)
不稳定
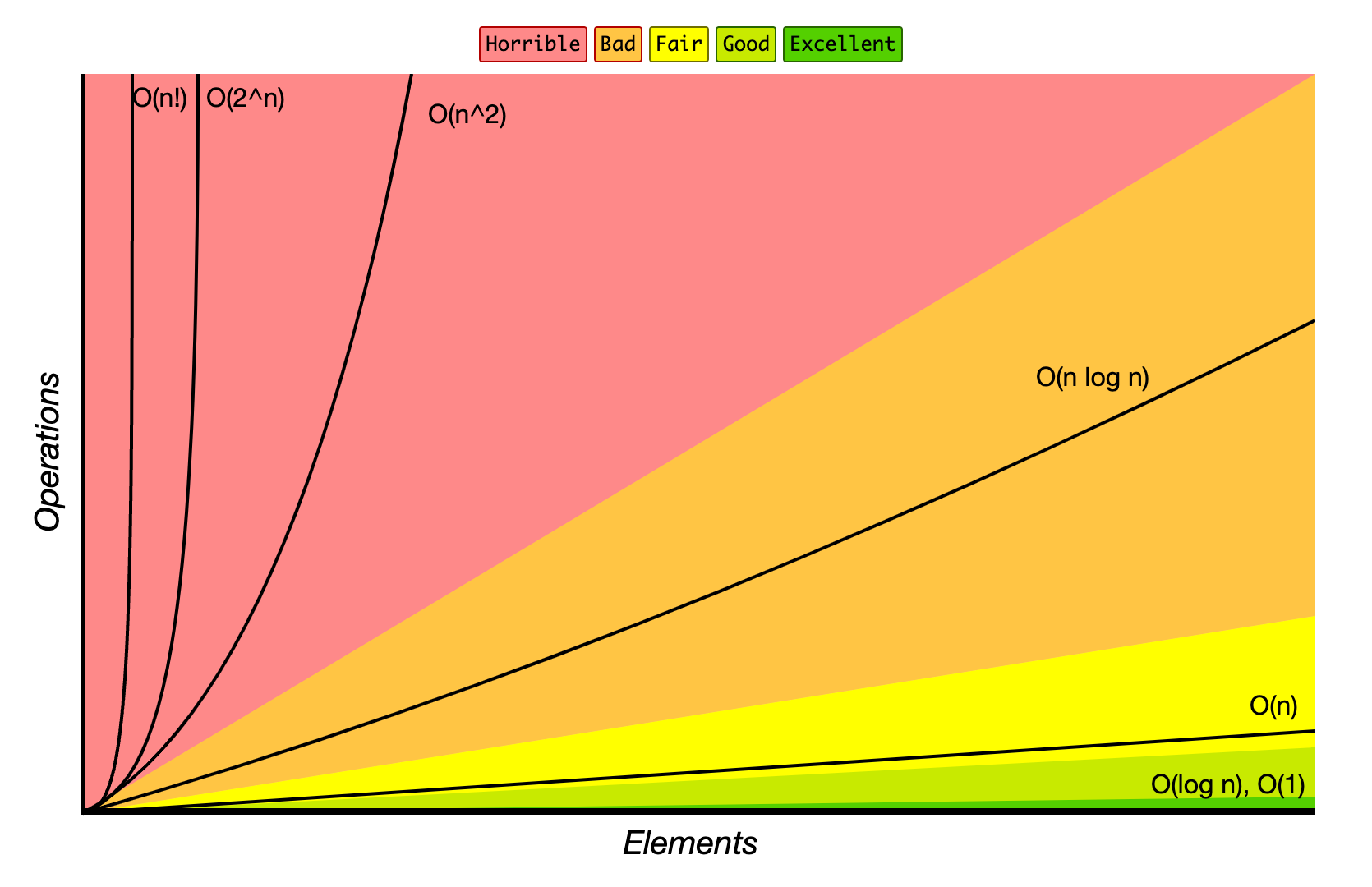
时间复杂度(time complexity)
用来描述算法的运行时间。常用大 O 符号表述。比如:O(n),O(1),O(logn),O(n^2)等。举例:
O(n)表示线性级复杂度,表示时间复杂度和元素 element 数量 n 成正比。比如数组的线性查找的复杂度随着元素数量增加而增加。
O(1)表示常数级复杂度,表示时间复杂度不随元素 element 数量变化而变化。比如链表的插入的复杂度不随链表节点数量变化而变化。
其他常见的复杂度如下图所示:
空间复杂度(Space Complexity)
对一个算法在运行过程中临时占用存储空间大小的量度。也可用大 O 符号表述。举例:
O(n)表示线性级复杂度,表示算法所需空间大小和元素数量成正比,比如归并排序,需要额外的临时空间来保存两个数组的合并结果,元素越多所需空间越大。
O(n)表示常数级复杂度,表示算法所需空间大小和元素数量无关。
排序的稳定性
冒泡排序(Bubble Sort)
动图
核心思路
将数组分为左右两部分,左为无序部分,右为有序部分。无序部分中的最大数在每次遍历结束后被交换到无序部分的最右侧,继而成为有序部分的最左侧元素,就像冒泡一样。
代码
func sort(_ a:inout Array[I]){
let n = a.count
for i in 0.. a[j+1] {
a.swapAt(j, j+1)
isSorted = false
}
}
if isSorted {
break
}
}
}
代码讲解
使用双重循来遍历,把双重循环分为内循环和外循环。
从左往右处理无序部分,使用下标 j 遍历,比较相邻元素大小,交换位置成为左小右大,一次遍历后,无序部分中最大数被交换到无序部分的最右处,继而加入有序部分的最左侧。
i 可理解为有序部分的数量,每次内循环结束,有序部分数量增加一个,无序部分数量减少一个。
特点
两两比较,不存在跳跃,所以稳定。
每次遍历都能检查数组是否有序,可提前退出排序,但是冒泡的交换在内循环,交换次数多。实际效率比选择排序低。
复杂度分析
最好的情况可以达到 O(n),最坏的情况是 O(n^2),平均 O(n^2)。
选择排序(Selection Sort)
动图
核心思路
将数组分为左右两部分,左为有序部分,右为无序部分。无序部分每次遍历选择出一个最小的元素,交换到无序部分的最左侧,继而成为有序部分的最右侧元素。
代码
func sort(_ a:inout Array[I]){
let n = a.count
for i in 0.. a[j] {
iMin = j
}
}
a.swapAt(i, iMin)
}
}
代码讲解
使用双重循来遍历,把双重循环分为内循环和外循环。
从左往右处理无序部分,使用下标 j 遍历,每次遍历后保存下无序部分中最小数的位置 iMin 。
i 为无序部分的首元素位置,其左侧为有序部分,将有序部分排除在内循环外。每次内循环结束,将内循环保存的 iMin 和 i 位置的连个元素交换,使有序部分数量增加一个,无序部分数量减少一个。
特点
由于交换动作放在外循环,交换次数少于冒泡,实际效率优于冒泡。除非本来就是有序的数组的最好情况,选择排序还是要进行比较和交换,而冒泡排序一次 n 的遍历就能提前退出。
不稳定,举个例子,序列 5 8 5 2 9 , 我们知道第一遍选择第 1 个元素 5 会和 2 交换,那么原序列中 2 个 5 的相对前后顺序就被破坏了)
复杂度分析
最好情况 O(n^2),最坏情况 O(n^2),平均 O(n^2)。
插入排序(Insertion Sort)
动图
核心思路
将数组分为左右两部分,左为有序部分,右为无序部分。遍历有序部分,将无序部分首元素,根据其大小在有序部分寻找合适的位置并插入。
代码
func sort(_ a:inout Array[I]){
let n = a.count
for i in 1.. 0 && a[hole-1] > value {
a[hole] = a[hole-1]
hole -= 1
}
a[hole] = value
}
}
代码讲解
使用双重循来遍历,把双重循环分为内循环和外循环。
每次从无序部分的首元素 value 的位置开始,从右向左,在有序部分中遍历,比较每一个元素,凡是比 value 大的元素,都向右移动一位,遍历结束后空出来的位置 hole 就是 value 的插入位置。
i 可理解为有序部分的数量,同时也是无序部分的首元素的位置。每次外循环 value 都作为无序部分首元素,需通过内循环在有序部分寻找一个合适的位置 hole 并将其插入。
特点
选择排序的比较开销是固定的 n(n-1)/2,而插入排序平均下来是 n(n-1)/4 。
选择排序最多只需要执行 2(n-1)次交换,而插入排序平均的交换开销也是 n(n-1)/4 。这就取决于单次比较和交换的开销之比。如果是一个量级的,则插入排序优于选择排序,如果交换开销远大于插入开销,则插入排序可能比选择排序慢。
两两比较,不存在跳跃,所以稳定。
复杂度分析
最好情况 O(n),最坏情况 O(n^2),平均 O(n^2)。
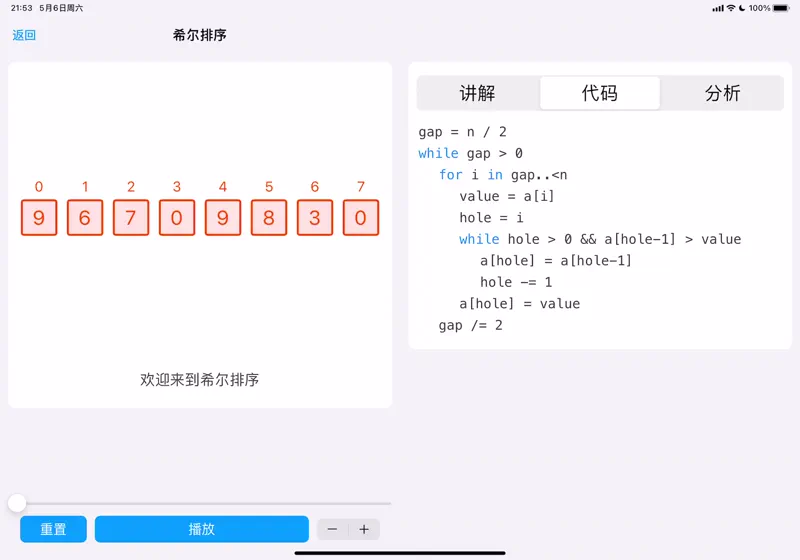
希尔排序(Shell Sort)
动图
核心思路
在插入排序基础上引入增量 gap 概念,是插入排序的改进。
代码
func sort(_ a:inout Array[I]){
let n = a.count
var gap = n / 2
while gap > 0 {
for i in gap.. 0 && a[hole-1] > value {
a[hole] = a[hole-1]
hole -= 1
}
a[hole] = value
}
gap /= 2
}
}
代码讲解
当增量 gap 为半数时,在整个数组中选取右边 1/2 部分进行插入排序,在此结果上在整个数组中选取右边 3/4 部分进行插入排序,反复这个过程,直到最后一次对整个数组做插入排序,最终成为有序数组。
每次做插入排序的部分从 gap 开始,每次扩大做插入排序的范围。
特点
希尔排序算法 1959 年提出,是直接插入排序算法的一种改进,减少了移动次数,平均时间复杂度比插入快。是第一批时间复杂度低于 O(n^2)的排序算法。
插入排序是稳定的,而 shell 排序会分组,相同的数分在不同的组内各自进行移动打破稳定性。所以不稳定。
复杂度分析
gap /= 2 表示折半的方式选取增量。究竟应该选取什么样的增量才是最好,目前还有数学上的定论。最坏的情况是 O(n^2),在使用了增量后,平均时间复杂度 O(n^(3/2))。
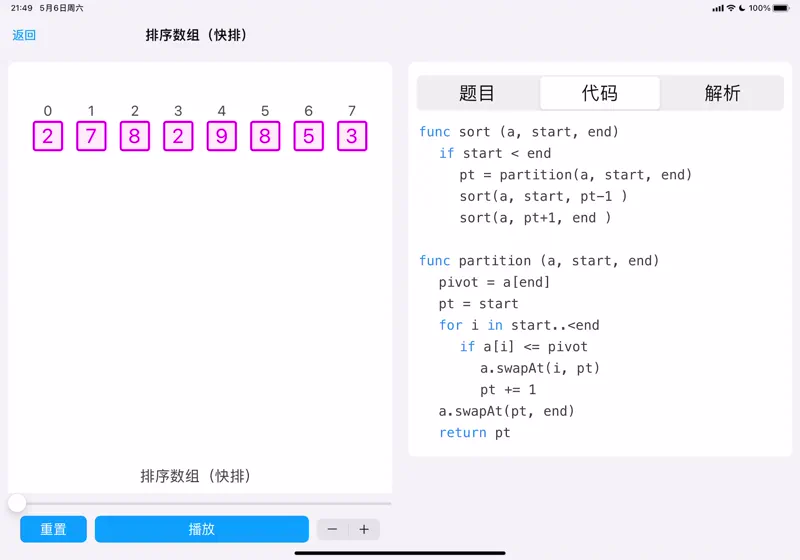
快速排序(Quick Sort)
动图
核心思路
将数组最右侧的元素作为一个参照值 pivot,以参照值为标准,将数组拆分 patition 为 3 个部分:比参照值小的部分,参照值,比参照值大的部分。
将这个过程再分别应用到较小部分和较大部分中继续拆分,直到所有部分被拆分成 1 个元素无法再拆分,就完成了排序。
这是一个分而治之的方法,也是一个递归的过程。
代码
func sort(_ a:inout Array[I], start: Int, end: Int){
if start Int {
let pivot = a[end]
var partitionIndex = start
for i in start..
代码讲解
每次递归将数组拆分成前部,基准值,后部 3 部分,前部比后部小。按此方法再递归调用前,后部分,最终达到从小到大的排序。
将数组 a 的 start 到 end 区间拆分为三部分。区间内选择一个参照值,通常可选 start 或者 end 的值为参照。因为区间拆分前无序,任何一个值都可作为参照,这里我们选择 end 的值作为参照值 pivot 。
因为 pivot 作为 end ,所以区间遍历使用 i 从 start 到 end-1 ,并假设参照值位置为 pt 初始为 start 。将比参照值小的元素交换到 pt ,pt 的右侧位置就是参照值的位置,所以 pt+=1 ,遍历结束,将参照值交换到 pt ,并返回参照值的位置。
调用 partition()拆分数组,返回拆分后参照值位置 pt ,那么数组前部分的区间是 start 到 pt-1 ,后部分的区间为 pt+1 到 end 。对着两部分继续递归调用 sort()。当数组被拆分为 1 个元素,即 start 等于 end 的时候,则停止分治,退出递归。
特点
快速排序是一种交换类的排序,它同样是分治法的经典体现。
如果 pivot 的值有重复,pivot 作为参照放在前后两部中间有可能打破稳定性,所以不稳定。
复杂度分析
待排序数组最终被拆分成深度为 logn+1 的二叉树。拆分次数为 logn 。第一次拆分时,总共的执行时间是 Cn(C 为固定的单位时间常数);第二次拆分时,每个子序列的执行时间为 Cn/2 ,总的执行时间是 Cn/2+Cn/2=Cn ;第三次拆分时,总时间时 Cn/4+Cn/4+Cn/4+Cn/4+=Cn ,所以每次执行复杂度都是 Cn 。
每次执行复杂度 Cn * 拆分次数 log(n) = 快排复杂度 O(nlogn)。最坏情况 O(n^2)。
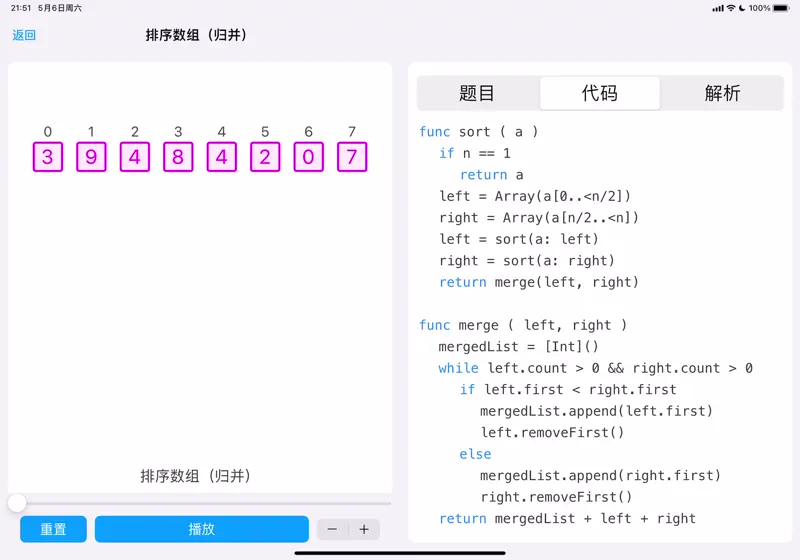
归并排序(Merge Sort)
动图
核心思路
将两个有序数组,合并为一个新的有序数组就是做归并。
归并排序中,将数组从中间分解为左右两部分,将这个过程再应用到左右部分中继续分解。最后把 n 个元素的数组分解为只有 1 个元素的 n 个数组。这种情况下,满足两个有序数组进行的归并条件,开始再两两归并,直到合并出一个新的有序数组就完成了排序。
这是一个分而治之的方法,同时也是一个递归的过程。
代码
func sort(a: [Int]) -> [Int] {
let n = a.count
if n == 1 {
return a
}
var left = Array(a[0.. [Int] {
var mergedList = [Int]()
while left.count > 0 && right.count > 0 {
if left.first!
代码讲解
特点
该算法采用经典的分治( divide-and-conquer )策略。分治法将问题分(divide)成一些小的问题然后递归求解。两两比较,不存在跳跃,所以稳定。
复杂度分析
归并排序的效率是比较高的,设数列长为 n ,将数列分开成小数列一共要 logn 步,每步都是一个合并有序数列的过程,时间复杂度可以记为 O(n),故一共为 O(nlogn)。对空间有要求,空间复杂度 O(n)。所以,归并排序是一种比较占用内存,但却效率高且稳定的算法。
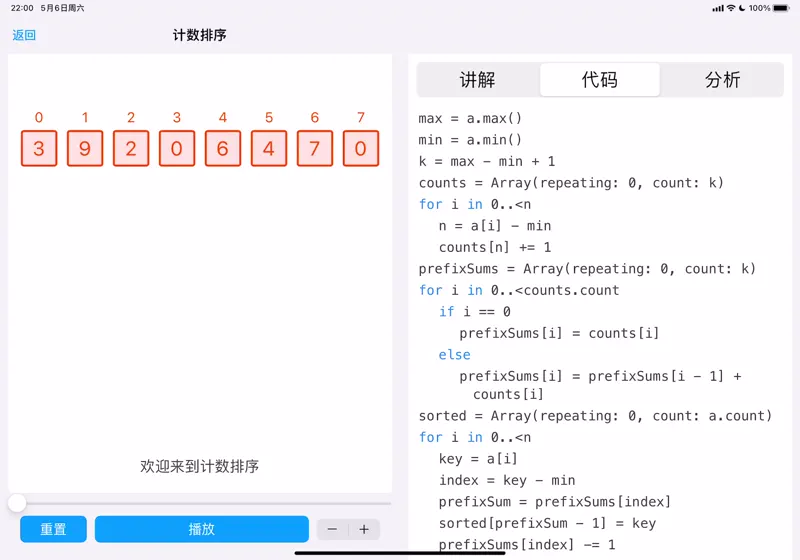
计数排序(Counting Sort)
动图
核心思路
通过前面元素出现的累计次数确定当前元素的位置,比如第一个元素 1 出现 3 次,那么元素 2 的位置从第 4 个开始,元素 2 出现 4 次,那么元素 3 的位置从第 8 个开始。
代码
func sort(_ a:inout Array[I]) {
let max = a.max() ?? 0
let min = a.min() ?? 0
let k = max - min + 1
var counts = [Int](repeating: 0, count: k)
for item in a {
let i = item - min
counts += 1
}
var prefixSums: [Int] = counts
for i in 1..
代码讲解
在无序数组中,先找出最大值 max 和最小值 min ,从而确定需要开辟 max-min+1 大小空间的计数数组和累计数组。
保存每个元素出现的次数。比如 1 出现 2 次,2 出现 3 次。
保存前面元素累计出现的次数。比如,1 出现 3 次,累计 3 次; 2 出现 4 次,累计 3+4=7 次; 3 出现 1 次,累计 7+1=8 次。累计次数-1 就是元素有序的位置。
特点
计数排序是一个稳定的非比较排序算法。它的优势在于在对一定范围内的整数排序,比如对 1 万名学生的考试分数做排序。计数排序是一种以空间换时间的排序算法,整数大小差异越大,所需要的空间越大。
复杂度分析
计数数组的大小为 k ,无序数组大小为 n ,复杂度为Ο(n+k),所以时间复杂度是 O(n);由于申请了大小为 k 的桶来放计数,所以空间复杂度是 O(k)。
基数排序(Radix Sort)
动图
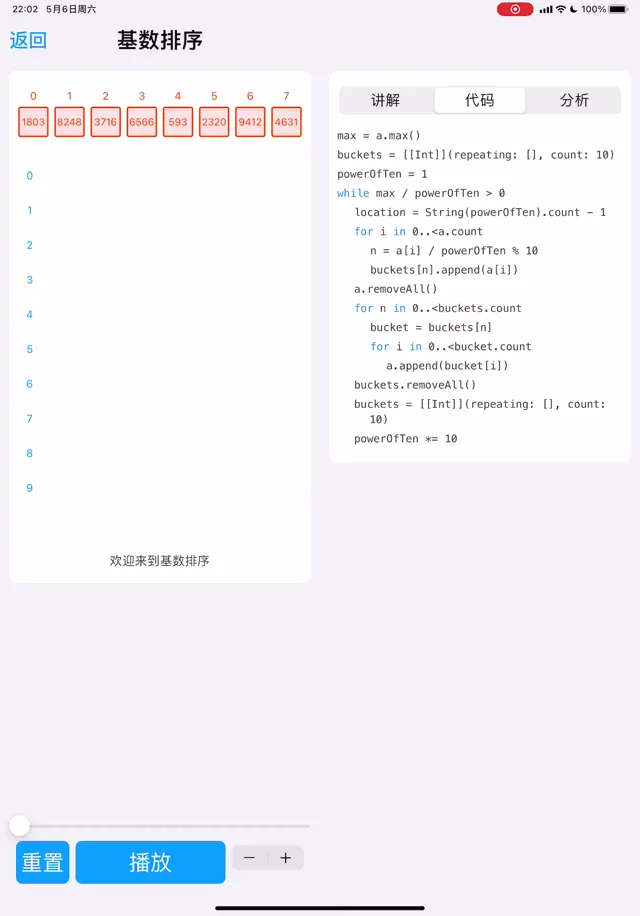
核心思路
是一种非比较的整数排序算法。其原理是将整数按位数切割成不同的数字,然后对每个位数上的数字进行分别比较。第一轮先按个位数大小排序,第二轮按十位数大小排序,一直进行到最高位。实际上是也一种桶排序,从 0 到 9 一共分 10 个桶。
代码
func sort(_ a:inout Array[I]){
let maxValue = a.max() ?? 0
var buckets = [[Int]](repeating: [], count: 10)
var powerOfTen = 1
while maxValue / powerOfTen > 0 {
a = a.compactMap { value in
buckets[value / powerOfTen % 10].append(value)
return nil
}
buckets = buckets.map { bucket in
bucket.forEach { value in
a.append(value)
}
return []
}
powerOfTen *= 10
}
}
代码讲解
先找到最大数,算出最大数有几位,则进行几次桶排序。
powerOfTen 初始为 1 ,每次 while 循环则乘以 10 倍,这样 while 循环的次数就是最大数的位数。
10 个桶,当进行个位数比较的时候,桶 n 保存个位为 n 的元素,当进行十位数比较的时候,桶 n 保存十位为 n 的元素。
特点
是一种非比较的稳定的整数排序算法。
不适用于数字的位数 k 多,但是排序的数少的情况;
适用于数字小但是排序的数字多的情况。
复杂度分析
复杂度是 O(n*k)。其中 n 是排序元素个数,每轮处理的操作数目; k 是数字位数,决定了进行多少轮处理。
并不一定优于 O(n·logn),当 k>logn ,就没有归并、堆排序快。
堆排序(Heap Sort)
相关概念:
动图
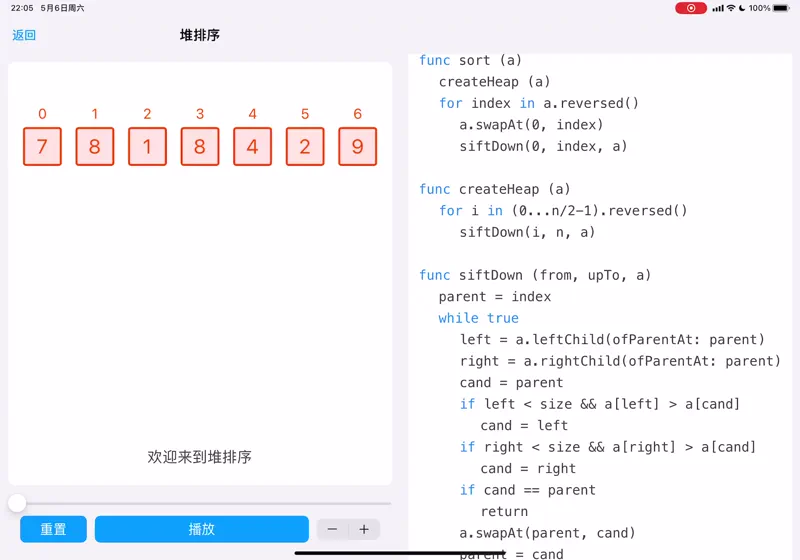
核心思路
大顶堆的顶是最大的,所以堆排序的过程就是反复的构造堆。
第一次构建的堆顶最大,和堆尾交换放在数组最后一位,第二次构建的堆的堆顶第二大,放在倒数第二位,以此类推进行排序。
代码
func sort(_ a:inout Array[I]){
// 构建初始堆
createHeap(a: &a)
// 重建堆。逆序遍历反复构建大顶堆,遍历一次,顶被摘掉放入结果数组 a 尾部,直到最后无法构建堆,结果就是有序数组 a
for index in a.indices.reversed() {
siftDown(from: 0, upTo: index, a: &a)
}
}
func createHeap(a:inout Array[I]) {
if !a.isEmpty {
//从 a.count/2 - 1 开始到 0 结束,逆序遍历。a.count/2 - 1 是第一个非叶子节点,向根部遍历
for i in stride(from: a.count/2 - 1, through: 0, by: -1) {
siftDown(from: i, upTo: a.count, a: &a)
}
}
}
func siftDown(from index: Int, upTo size: Int, a:inout Array[I]) {
var parent = index
while true {
let left = a[leftChildIndex(ofParentAt: parent)]
let right = a[rightChildIndex(ofParentAt: parent)]
var candidate = parent
if left a[candidate] {
candidate = left
}
if right a[candidate] {
candidate = right
}
if candidate == parent {
return
}
a.swapAt(parent, candidate)
parent = candidate
}
}
// 在树的顺序存储中,返回 i 的左子节点的下标
func leftChildIndex(ofParentAt i: Int) -> Int {
return (2 * i) + 1
}
// 在树的顺序存储中,返回 i 的右子节点的下标
func rightChildIndex(ofParentAt i: Int) -> Int {
return (2 * i) + 2
}
代码讲解
先构建堆,可以是大顶堆(也可以是小顶堆)。交换堆顶[0]元素(堆中最大)与末尾[index]元素,再将[0 ,--index]的堆调整为大顶堆。重复到 index 为 0 。
特点
堆尾如果有重复,被交换到数组首再构建堆,会打破稳定性,所以不稳定(记录的比较和交换是跳跃式进行的)。
复杂度分析
整体主要由构建初始堆和重建堆两部分组成。其中构建初始堆经推导复杂度为 O(n),在交换并重建堆的过程中,需交换 n-1 次;而重建堆的过程中,根据完全二叉树的性质,[log2(n-1),log2(n-2)...1]逐步递减,近似为 nlogn 。所以堆排序时间复杂度一般认为就是 O(nlogn)级。,空间复杂度是 O(1)。

