声明
本文章中所有内容仅供学习交流,抓包内容、敏感网址、数据接口均已做脱敏处理,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关,若有侵权,请联系我立即删除!
本文章未经许可禁止转载,禁止任何修改后二次传播,擅自使用本文讲解的技术而导致的任何意外,作者均不负责,若有侵权,请联系作者立即删除!
逆向目标
目标:某验三代滑块验证码,底图还原及 w 参数逆向
验证码 demo 列表:aHR0cHM6Ly93d3cuZ2VldGVzdC5jb20vZGVtby8=
滑块验证码:aHR0cHM6Ly93d3cuZ2VldGVzdC5jb20vZGVtby9zbGlkZS1mbG9hdC5odG1s
加密算法:RSA、AES、MD5
验证码流程分析
进入网页后,打开开发者人员工具进行抓包
1.未点击按钮进行验证之前,Network 中抓包到了以下信息:
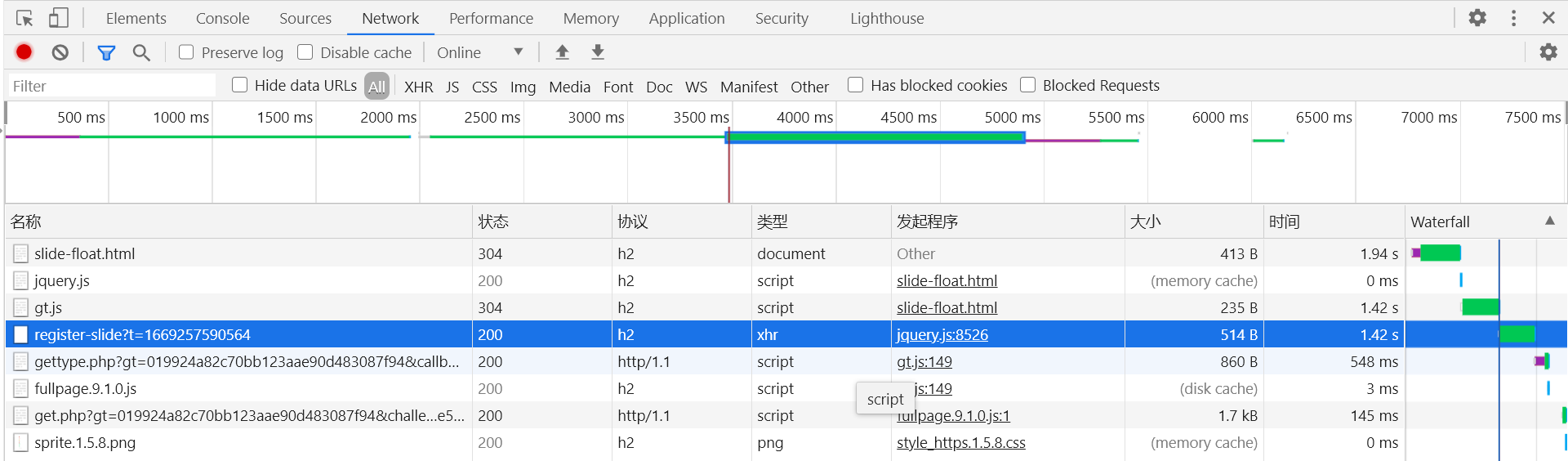
注册滑块请求,响应预览中返回的信息中重要的是 gt 和 challenge,gt 是固定值,不同网页对应不同的 gt 值,类似于特征码,challenge 的值每次刷新页面都会变化,gt 参数会通过 url string 的形式传递给 gettype.php:
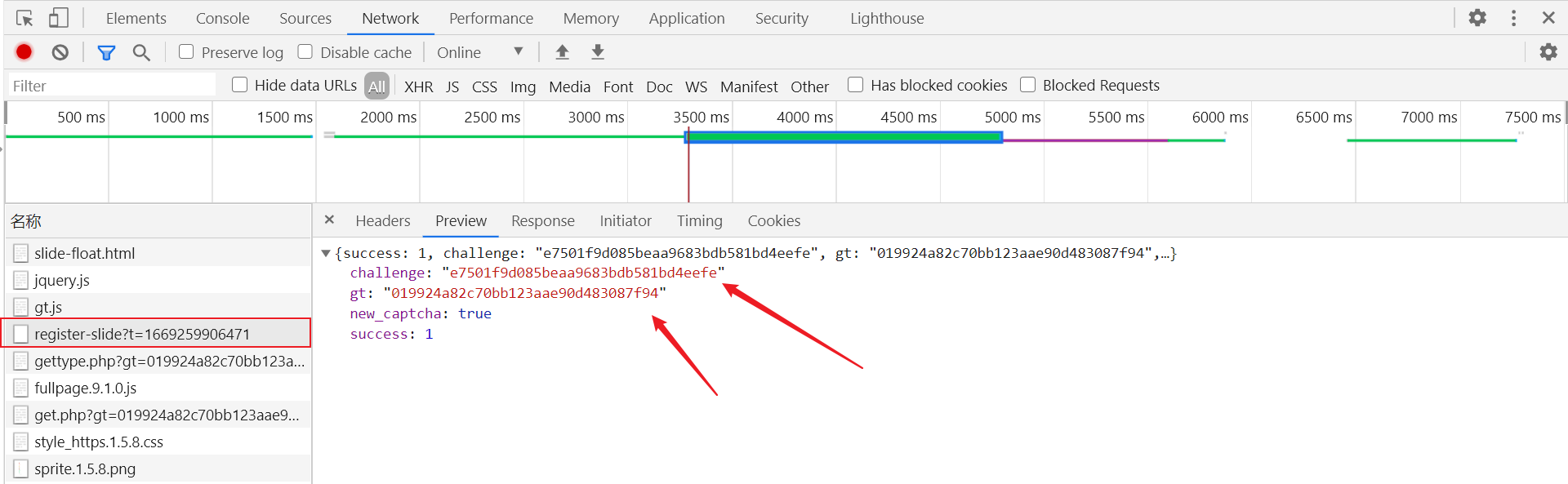
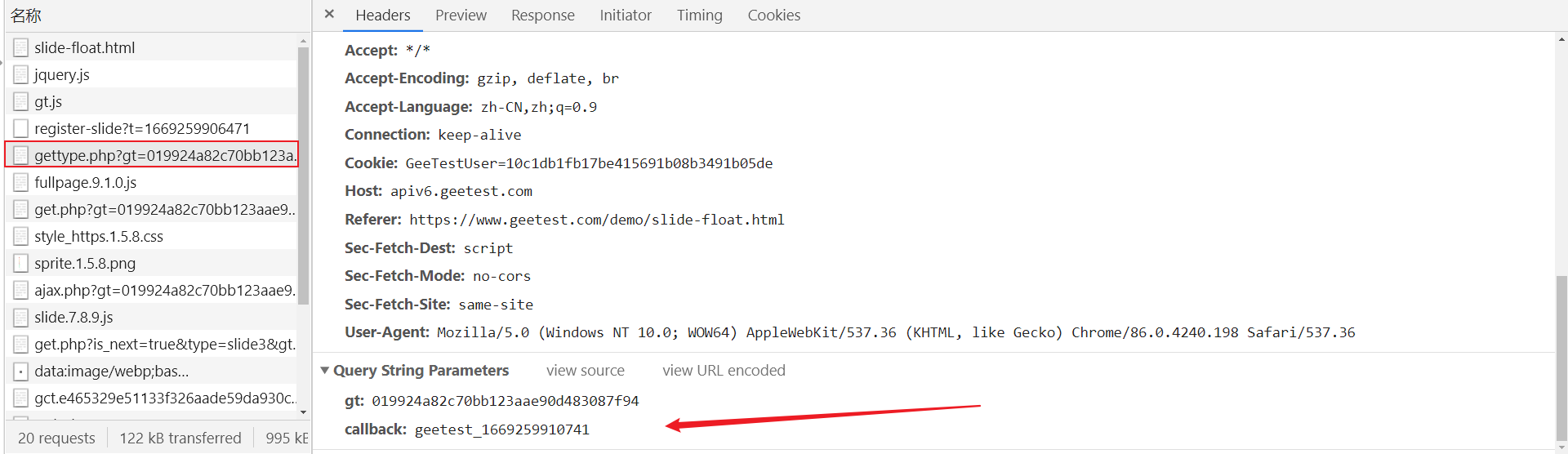
获取验证码,HTTP 请求中不同的请求方式和设置不同的 Content-Type 时,参数传递的方式会不一样,一般为 Query String Parameters、Form Data、Request Payload,这里是 Query String Parameters,在 GET 请求时,参数会以 url string 的形式进行传递,即 ? 后的字符串则为其请求参数,并以 & 作为分隔符,这里传递了 gt 参数的值以及 callback,callback 为 geetest_ + 时间戳:
响应预览中返回了一些 js 文件及对应的版本号:
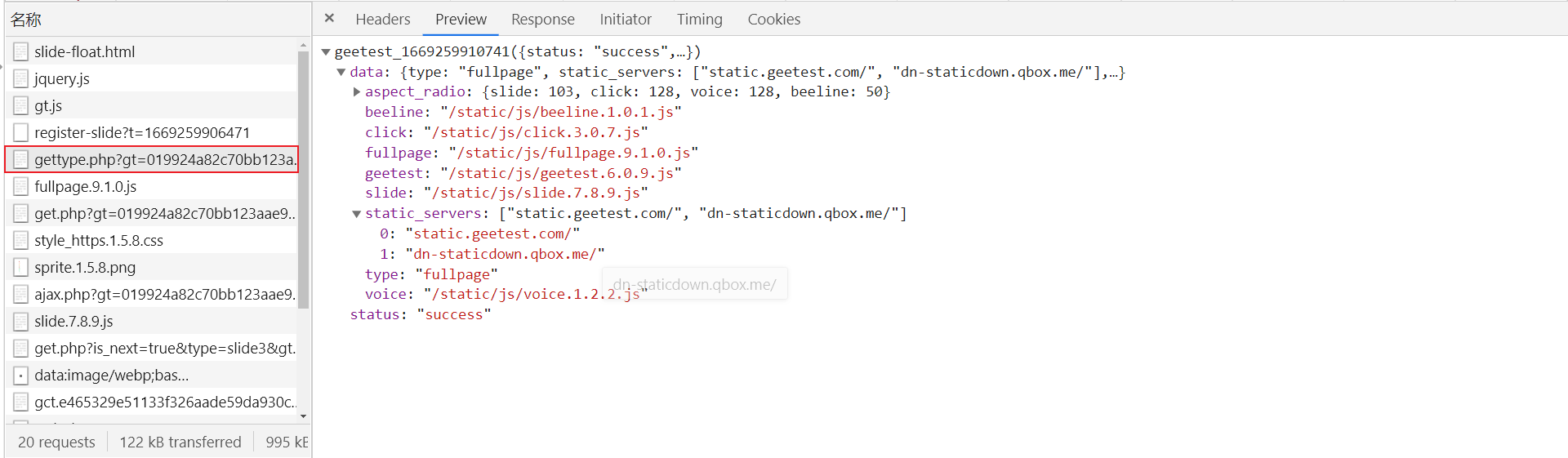
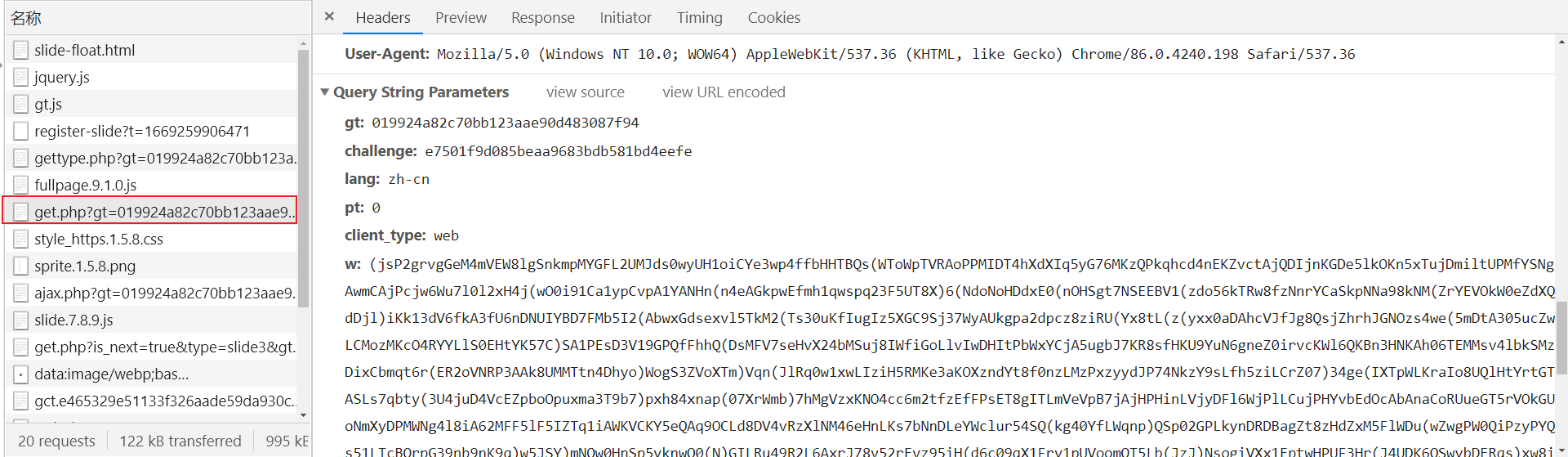
第一个 get.php?xxx,url 中传递了一些参数,关键部分如下:
响应内容如下,这里没什么需要注意的,feedback 就是某验的帮助中心:
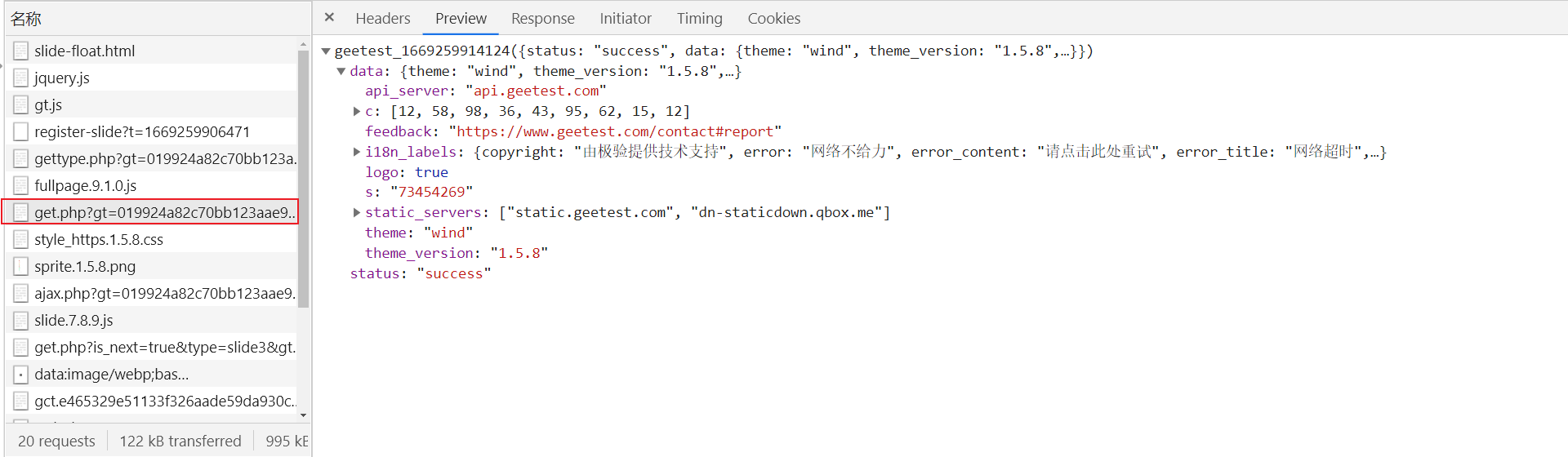
2.点击按钮进行验证之后,Network 中抓包到了以下信息:

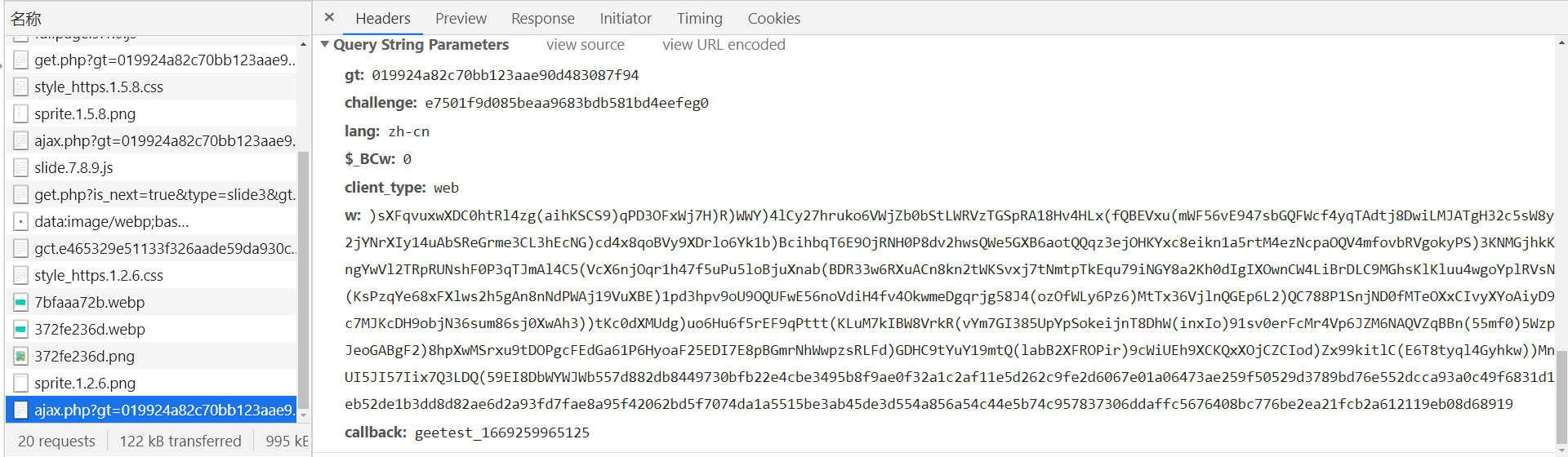
第一个 ajax.php?xxx,url 中传递了一些参数,关键部分如下:
gt:register-slide 响应返回的 gt 值
challenge:register-slide 响应返回的 challenge 值
w:对轨迹、滑动时间等进行加密后的参数,该网站第二个 w 值也可以直接置空
callback:geetest_ + 时间戳
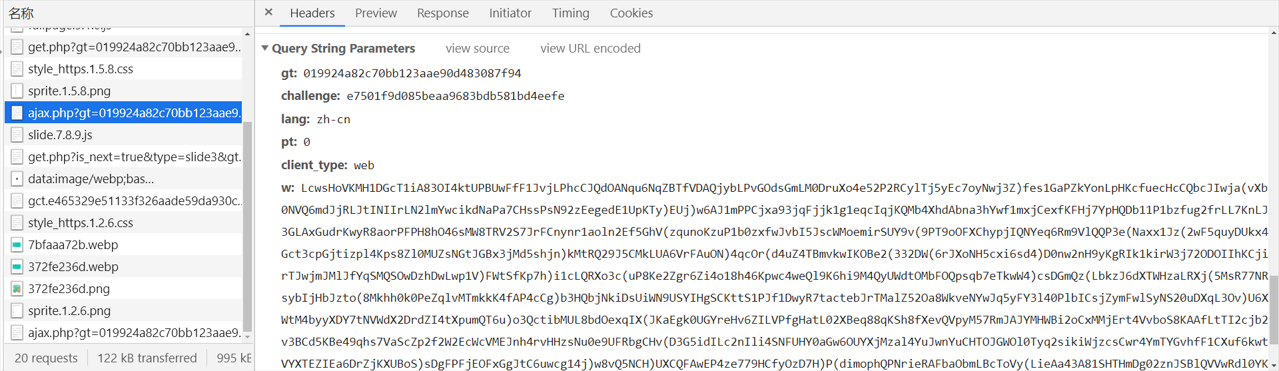
响应返回验证码模式,滑块验证码为 slide,点选验证码为 click:

第二个 get.php?xxx,url 中传递了一些参数,关键部分如下:
这个响应返回了很多关键内容:
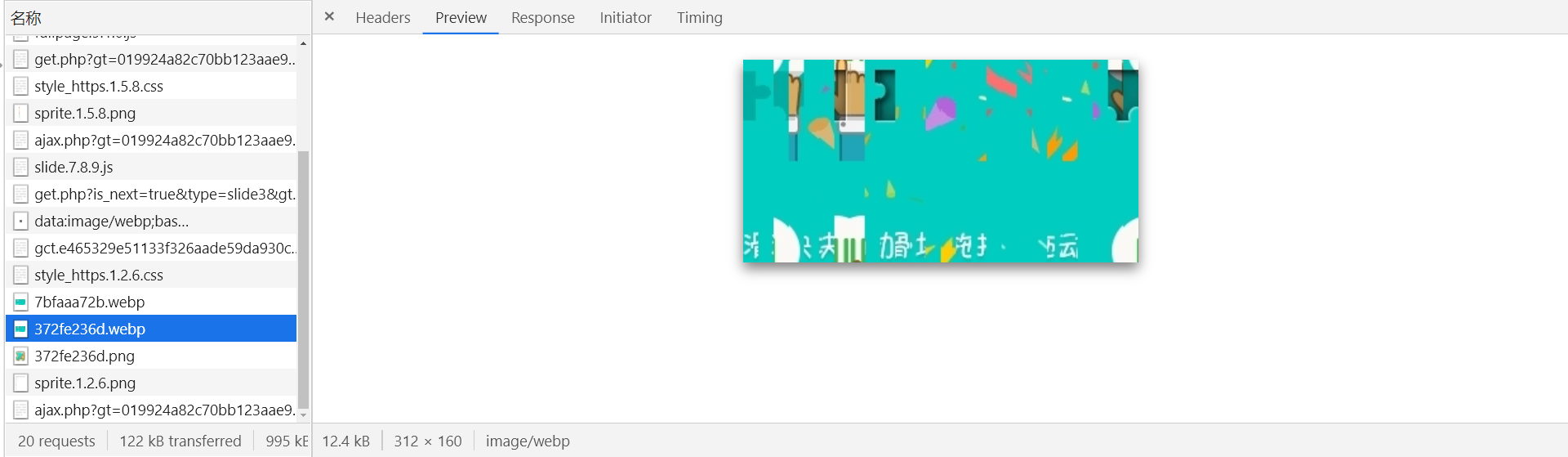
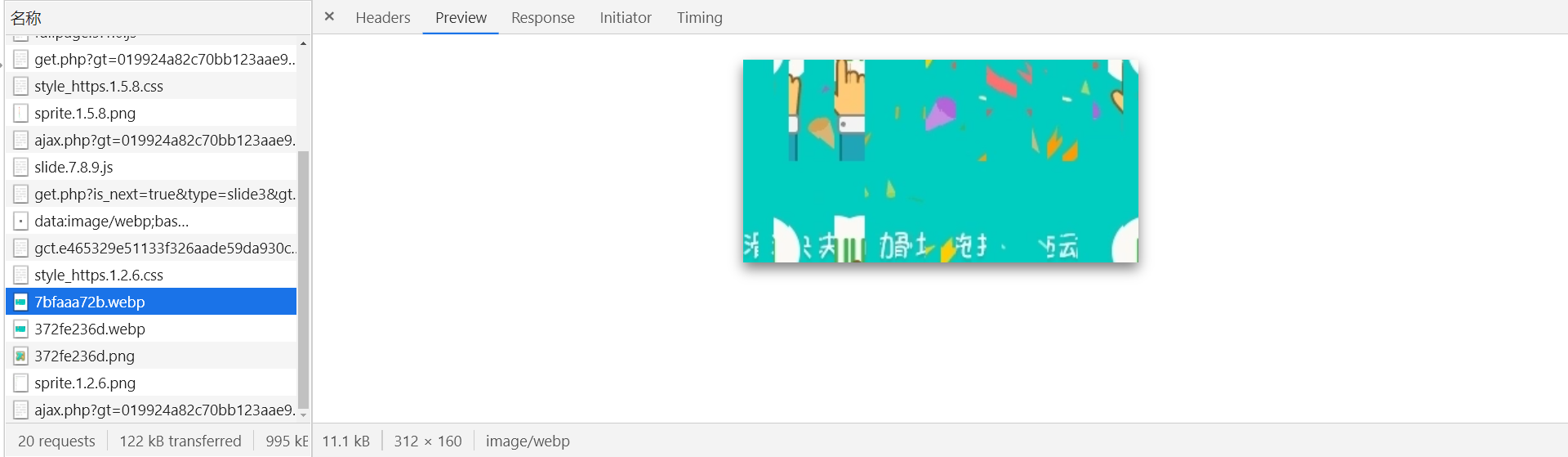
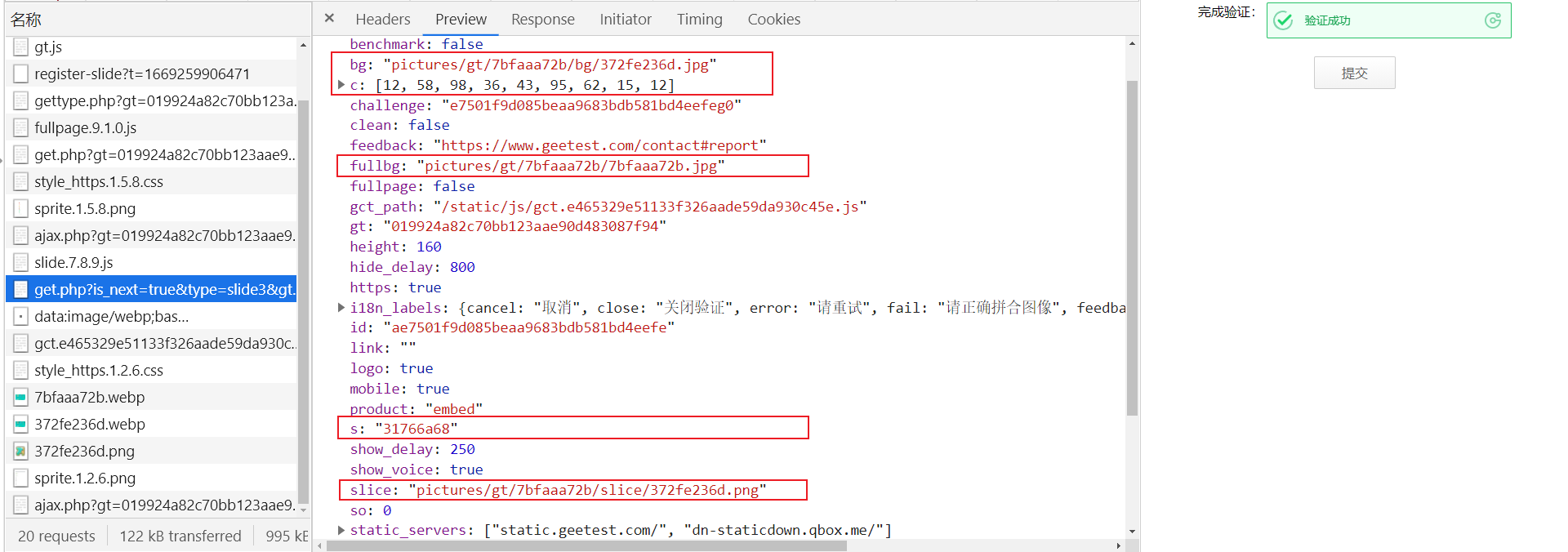
第二个 ajax.php?xxx,url 中传递了一些参数,关键部分如下:
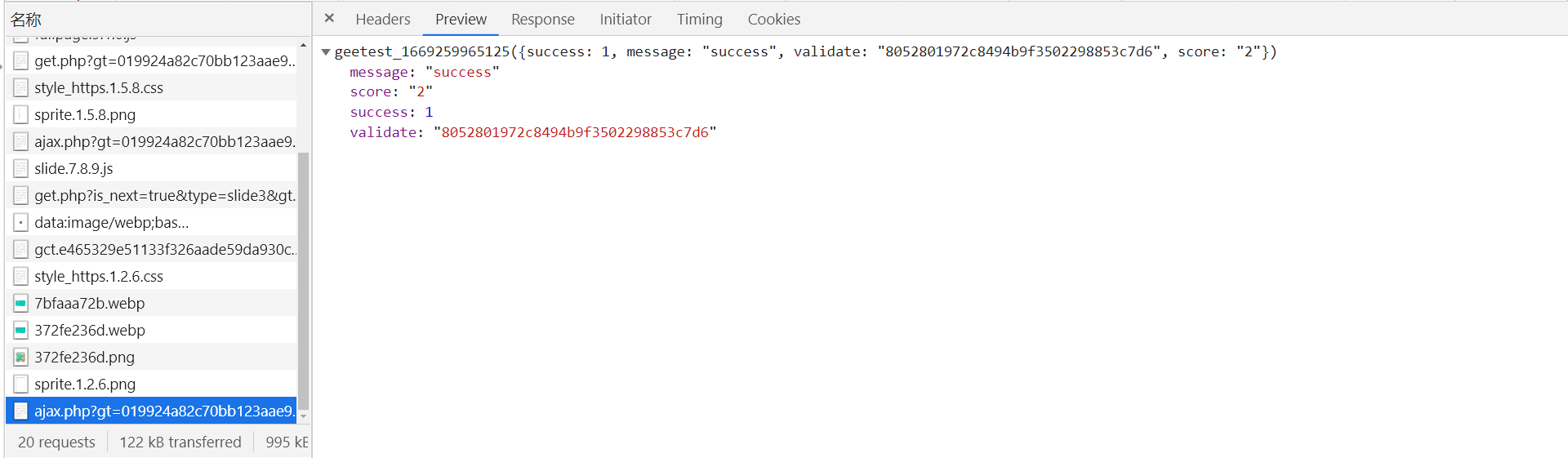
滑动滑块验证通过即会返回以下内容:
失败则会返回:
逆向分析
w 参数
跟到 w 参数的值方法很多,以下讲两种:
1.很简便,w 参数在 js 文件中有特征码,点击按钮进行验证之后,ctrl + shift + f 全局搜索 "\u0077",然后点击进入 slide.7.8.9.js 文件中,7.8.9 为当前版本,注意没点击验证的话是不会有这个 js 文件的:
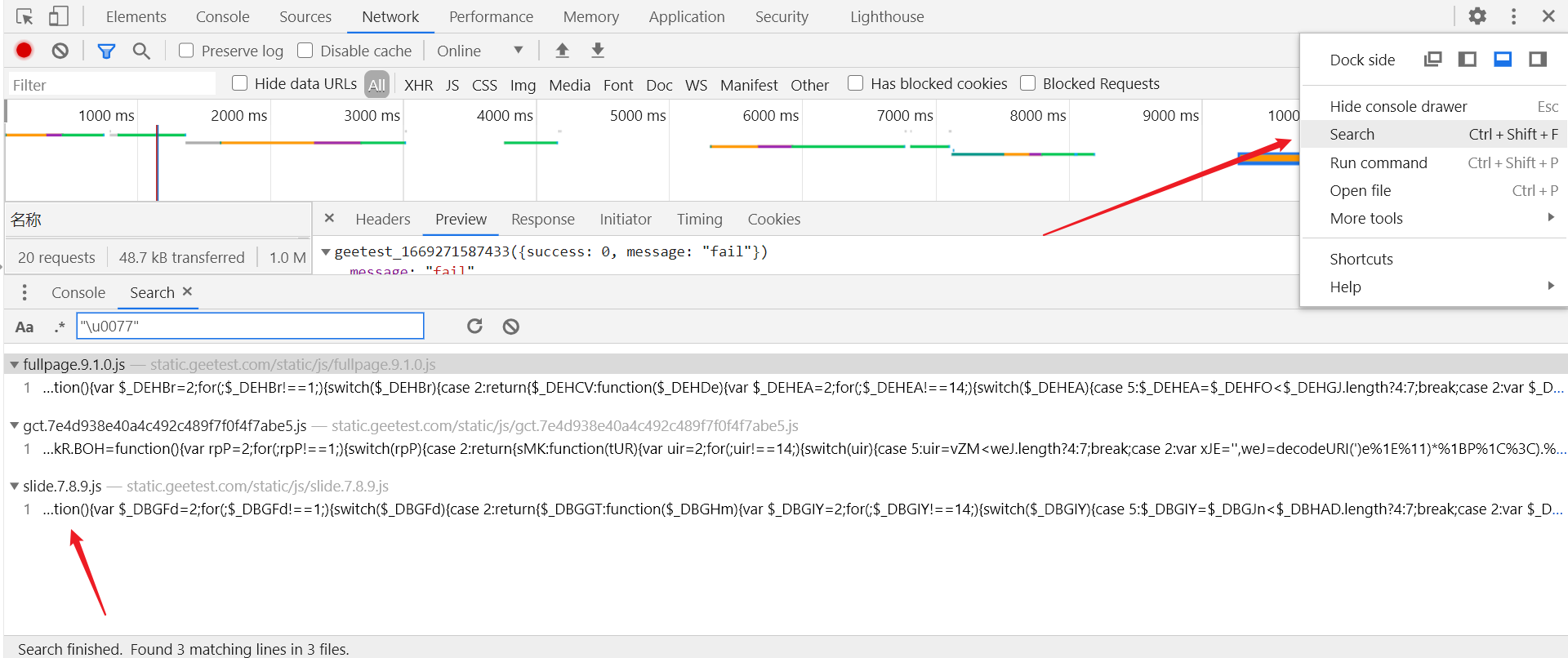
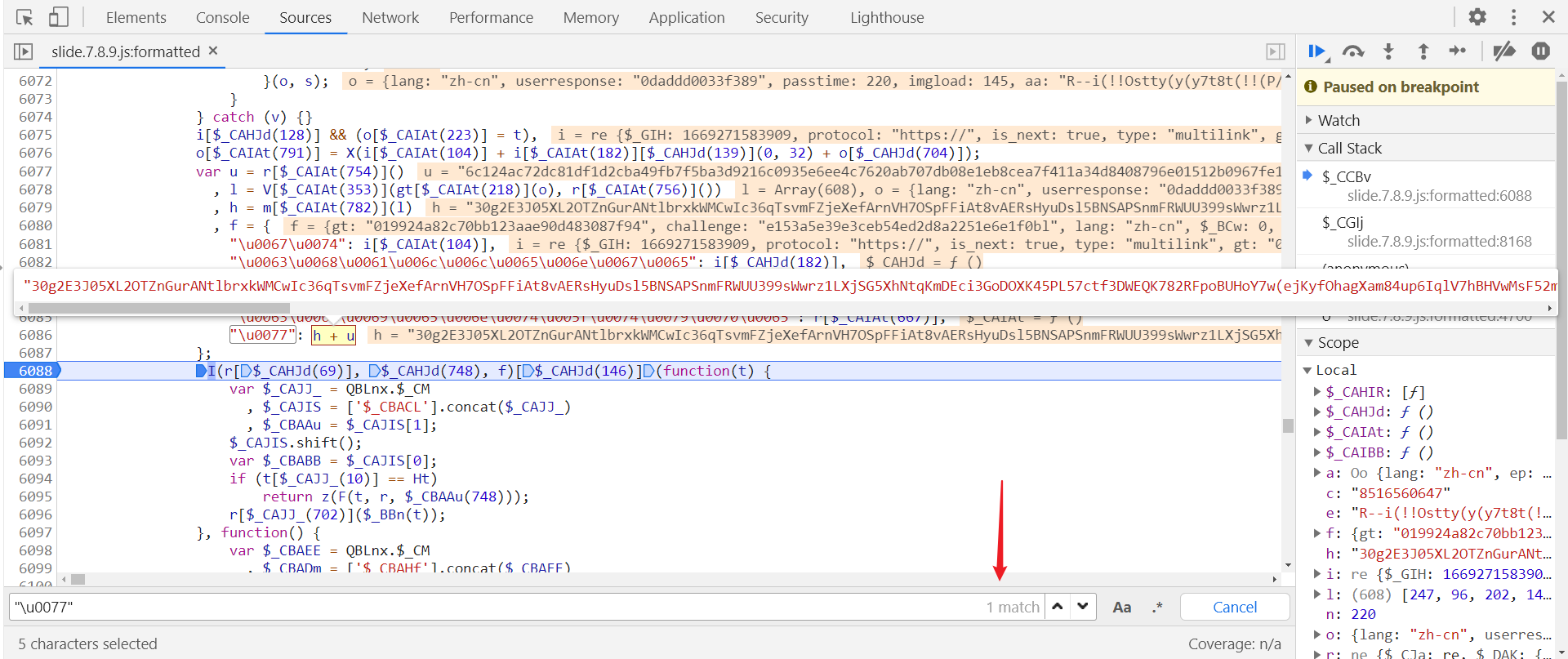
进入后点击左下角 { } 大括号,格式化文件,再 ctrl + f 局部搜索 "\u0077",只有一个结果,在第 6086 行,在第 6088 行打下断点,滑动滑块即会断住,h + u 即为 w 参数的值:
2.通过 Initiator 跟栈,跟进到 $_CId 中:
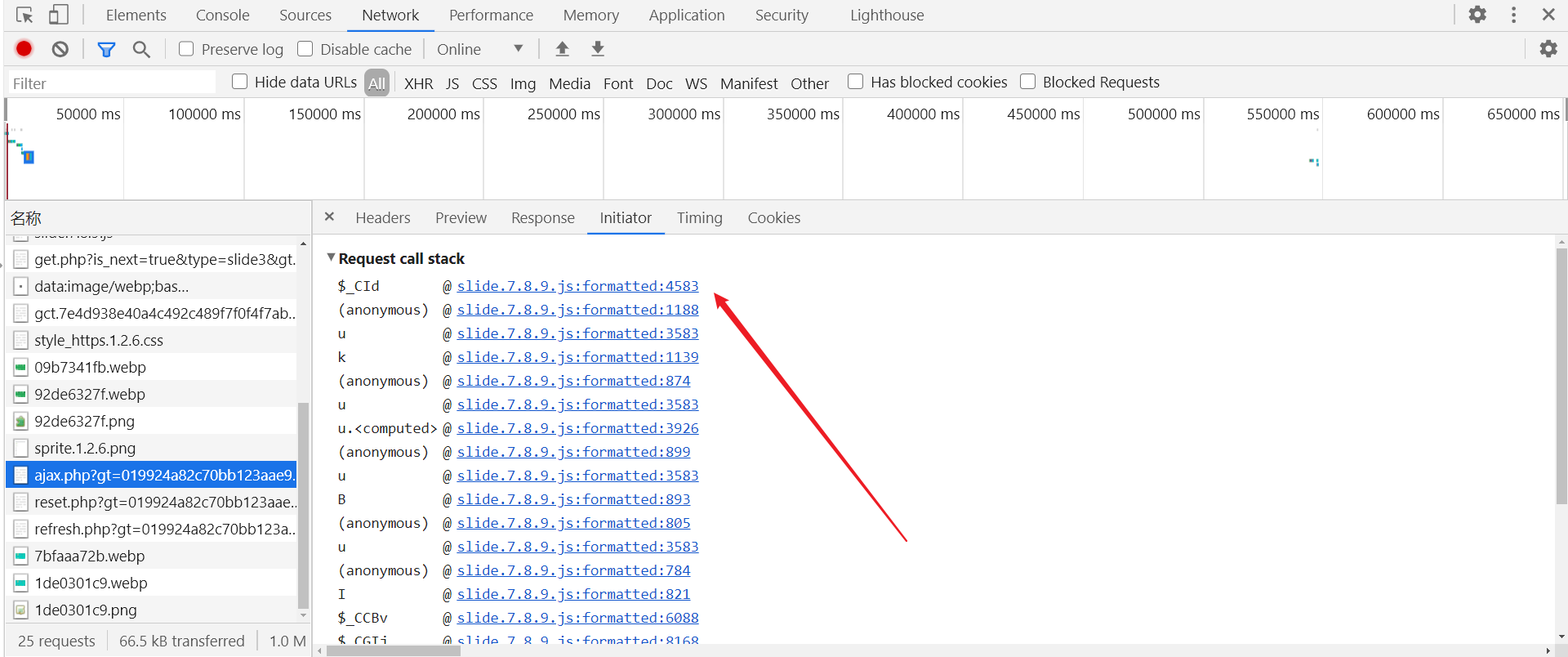
进去同样格式化后,会跳转到第 4583 行,在该行打下断点:
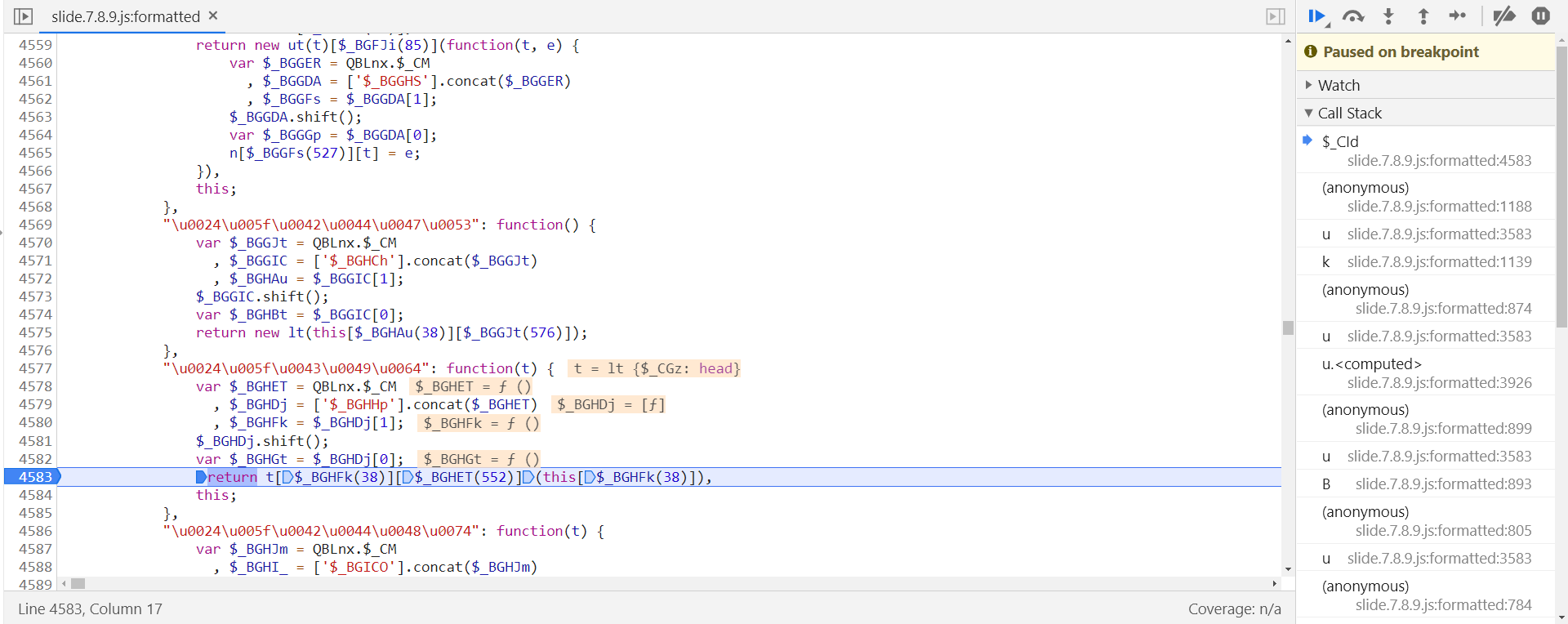
向上跟栈到 $_CCBv 中同样会找到刚刚的位置:

由以上分析可知,w 参数是 h 和 u 相加得到的,所以找到定义的位置,看看是怎么构造生成的,u 参数定义在第 6077 行,h 参数定义在第 6079 行,内容如下:
var u = r[$_CAIAt(754)]()
, l = V[$_CAIAt(353)](gt[$_CAIAt(218)](o), r[$_CAIAt(756)]())
, h = m[$_CAIAt(782)](l)
可以看到,h 参数是传入了 l 参数后经过 m[$_CAIAt(782)] 方法处理后得到的,所以依次往下分析,现在看看 u 参数是怎么生成的:
u 参数
u 参数通过 r[$_CAIAt(754)] 方法生成,选中后跟进到方法定义位置:
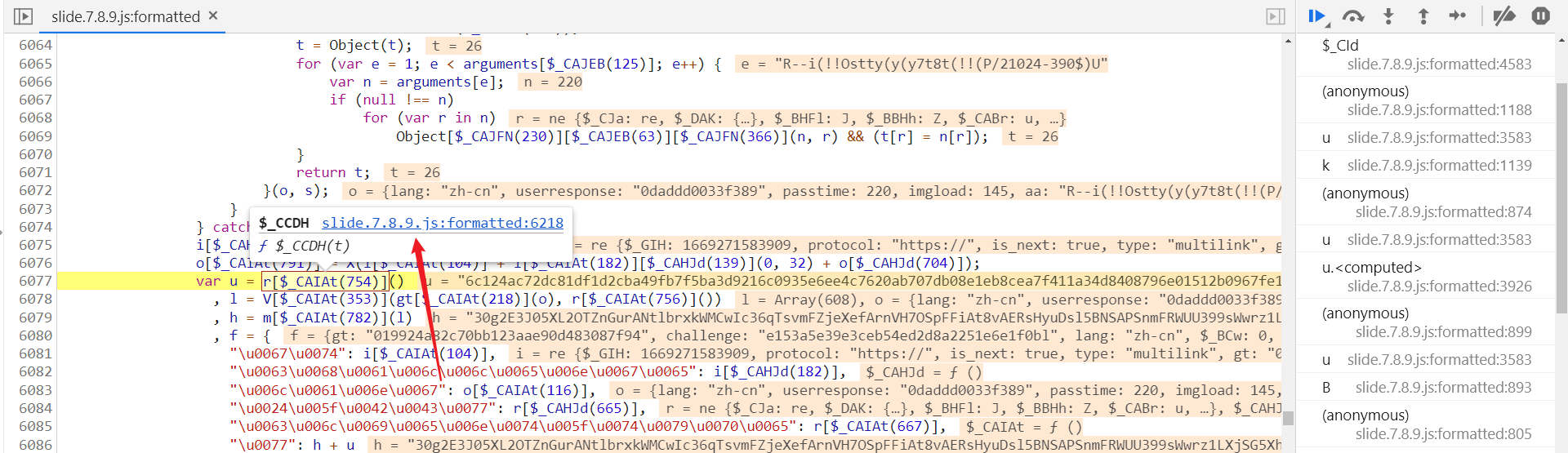
会跳转到第 6218 行,在 6227 行 return 处打下断点,重新拖动滑块,即会断住:
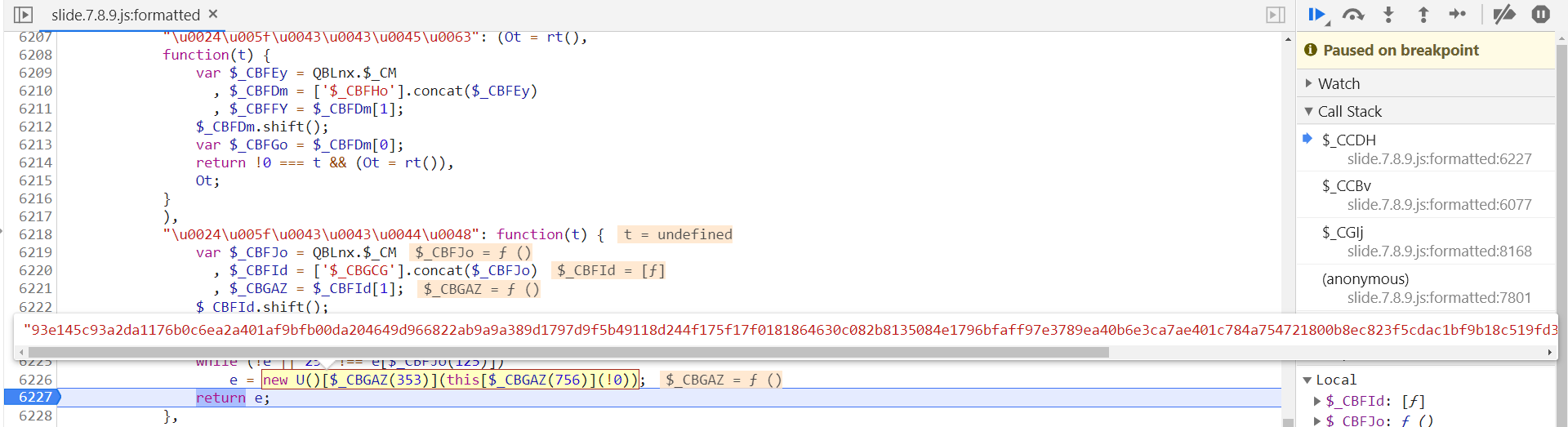
e 为 u 参数的值,其定义在第 6266 行:
e = new U()[$_CBGAZ(353)](this[$_CBGAZ(756)](!0));
在控制台中打印输出一下各部分内容:
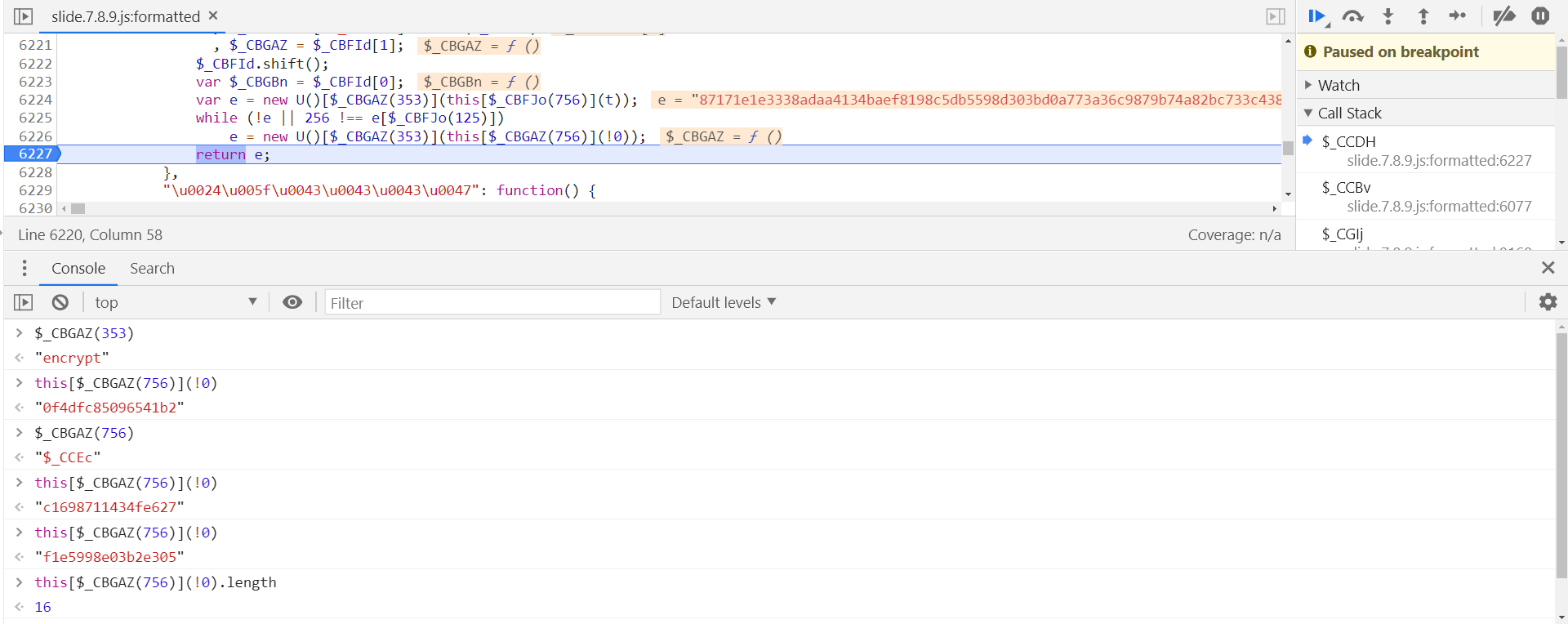
e = new U()["encrypt"](this["$_CCEc"](!0));
从打印出来的结果可以看出,e 参数的值可能是将 16 位的随机字符串加密后得到的,跟进到 this[$_CBGAZ(756)] 中验证一下:
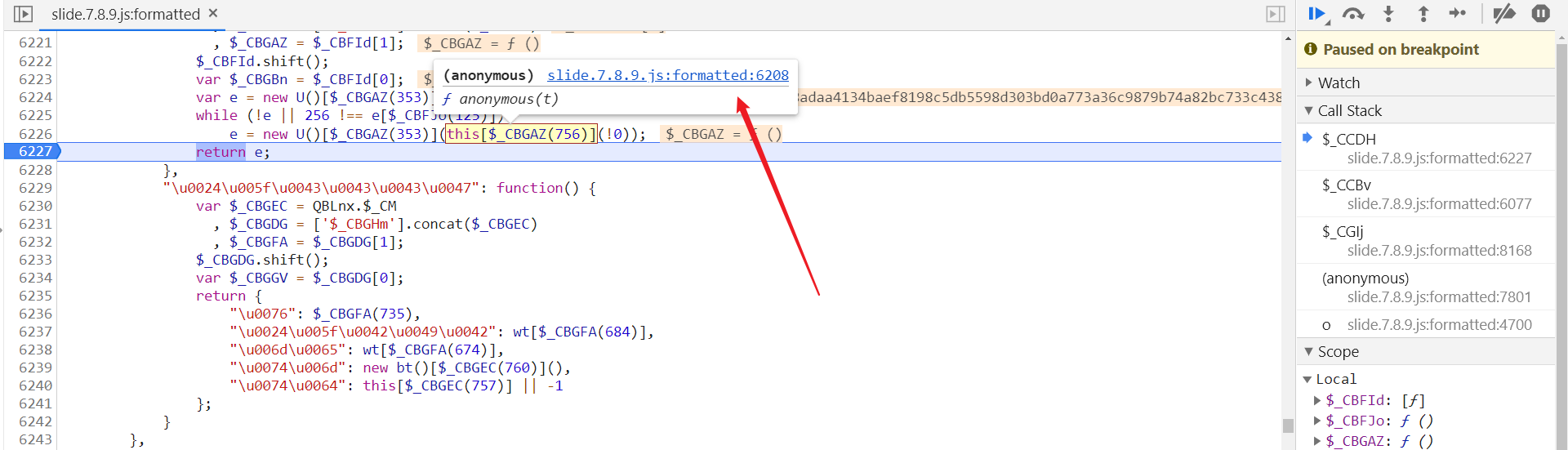
跳转到第 6208 行,在第 6214 行 return 处打下断点:
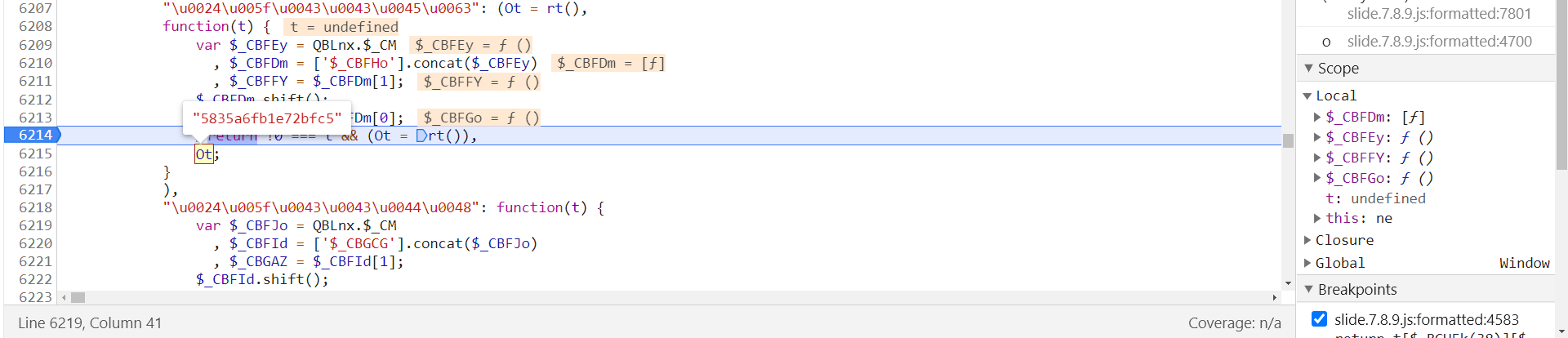
Ot 即 16 为字符串,Ot = rt(),跟进到 rt 函数中,在第 4213 行,于第 4219 行打下断点后会发现,16 位字符串是由四个 t() 方法的结果相加得到的:
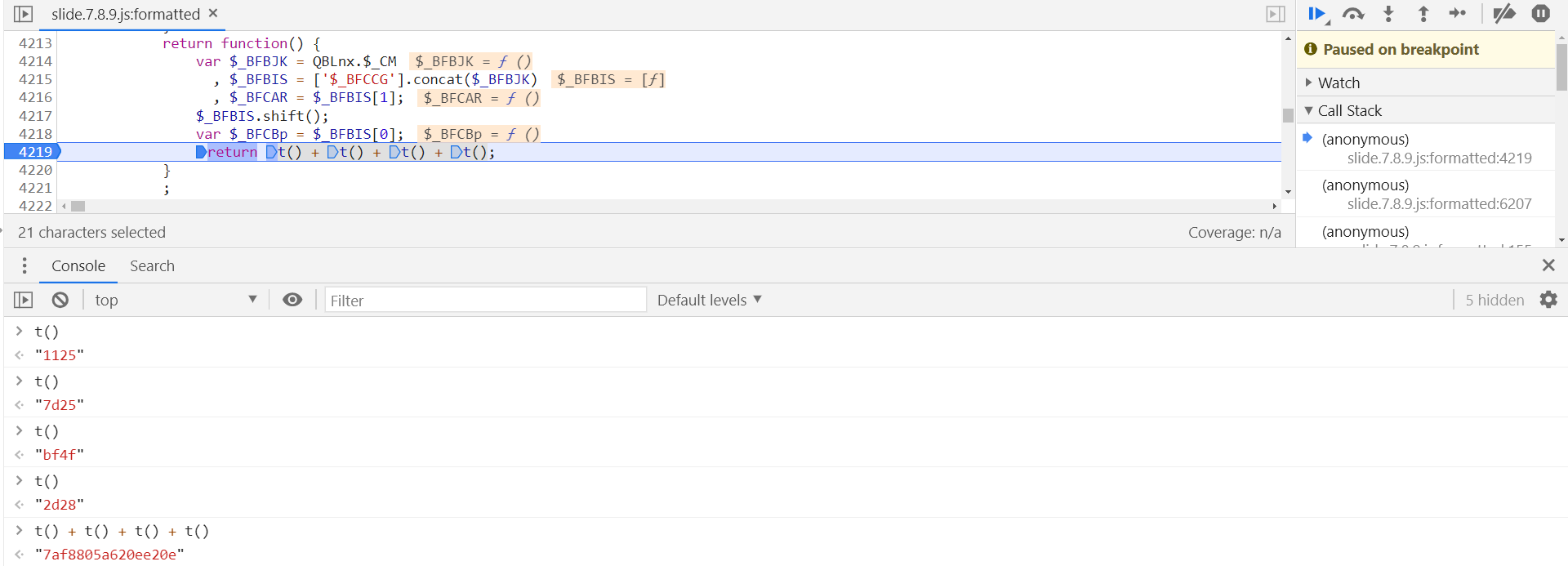
跟进到 t() 方法的定义位置,在第 4203 行,第 4208 行即为随机字符串算法:
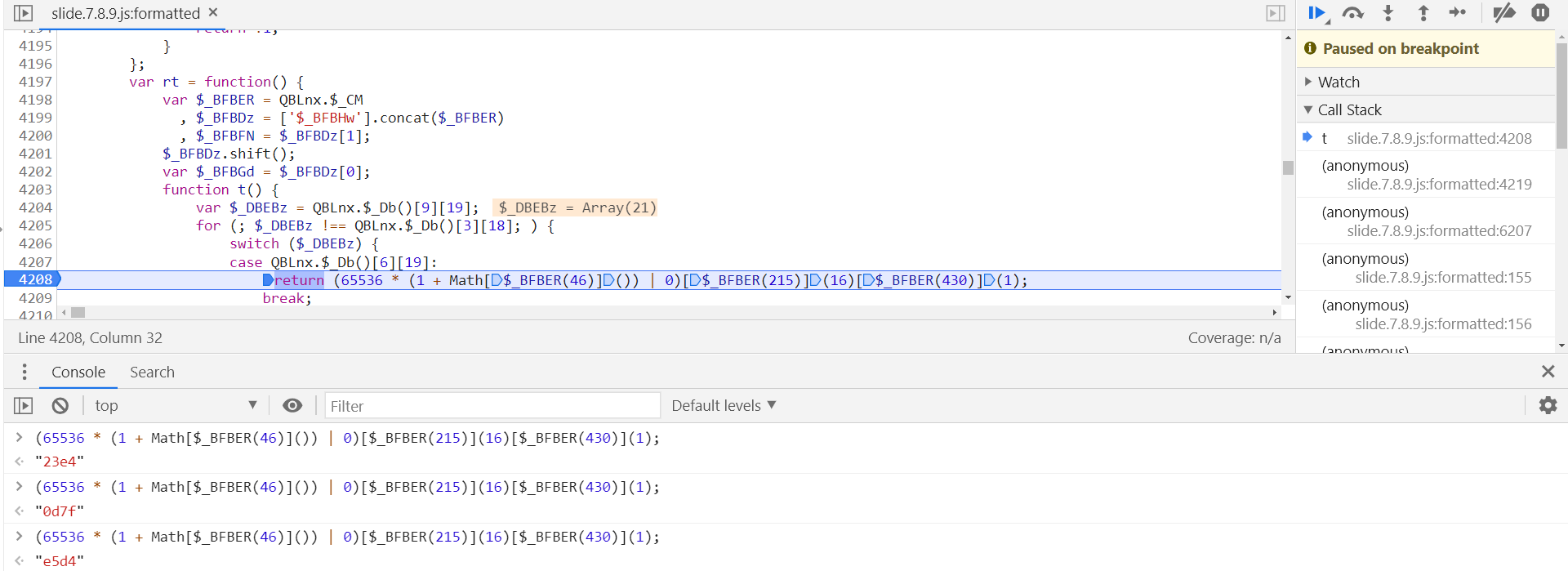
还原混淆后内容如下,Math.random() 是随机选取大于等于 0.0 且小于 1.0 的伪随机 double 值,toString(16) 为十六进制字符串:
(65536 * (1 + Math["random"]()) | 0)["toString"](16)["substring"](1)
JavaScript 复现:
function random() {
var random_str = "";
for (var index = 0; index
this["$_CCEc"] 分析完了,那 new U()["encrypt"] 是什么呢,选中 new U() 后,从原型链中可以看到 setPublic,根据经验很有可能就是 RSA 加密设置公钥,加解密相关算法可以查看 K 哥往期文章 【爬虫知识】爬虫常见加密解密算法:
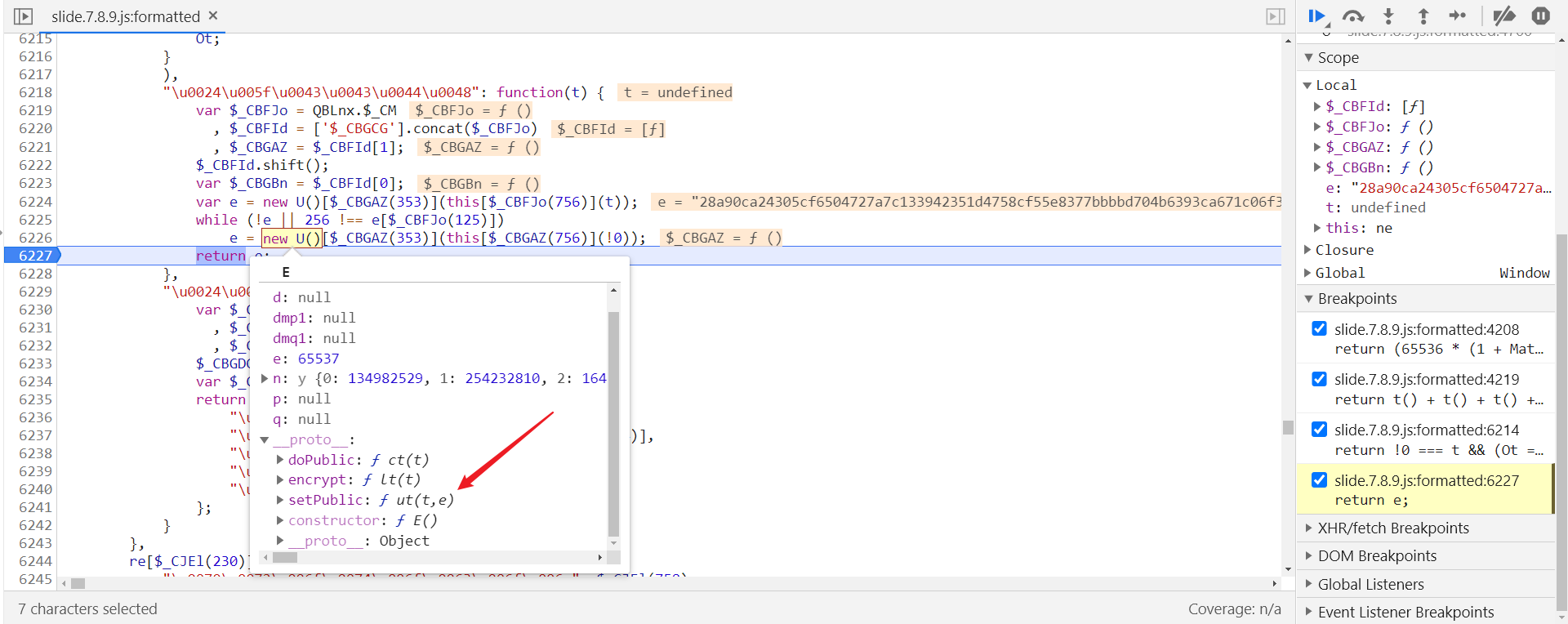
跟进去查看一下:
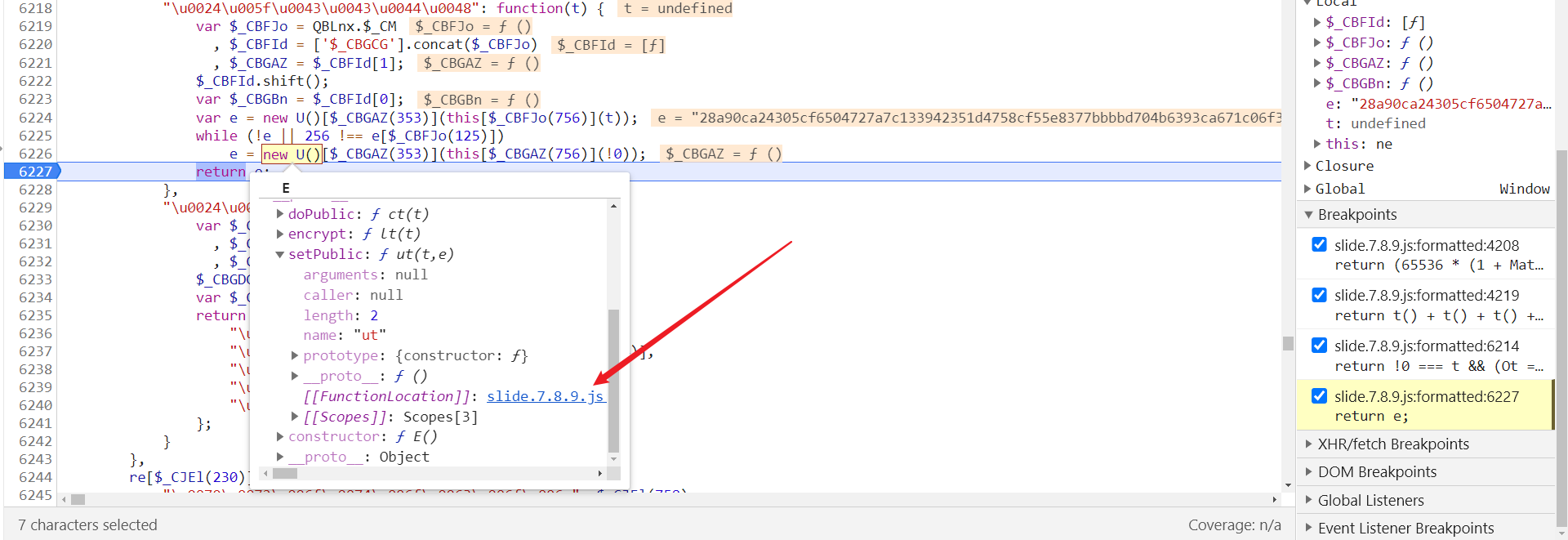
跳转到第 2908 行,在第 2922 行断住后,$_BACAs(332) 的值为 "Invalid RSA public key":
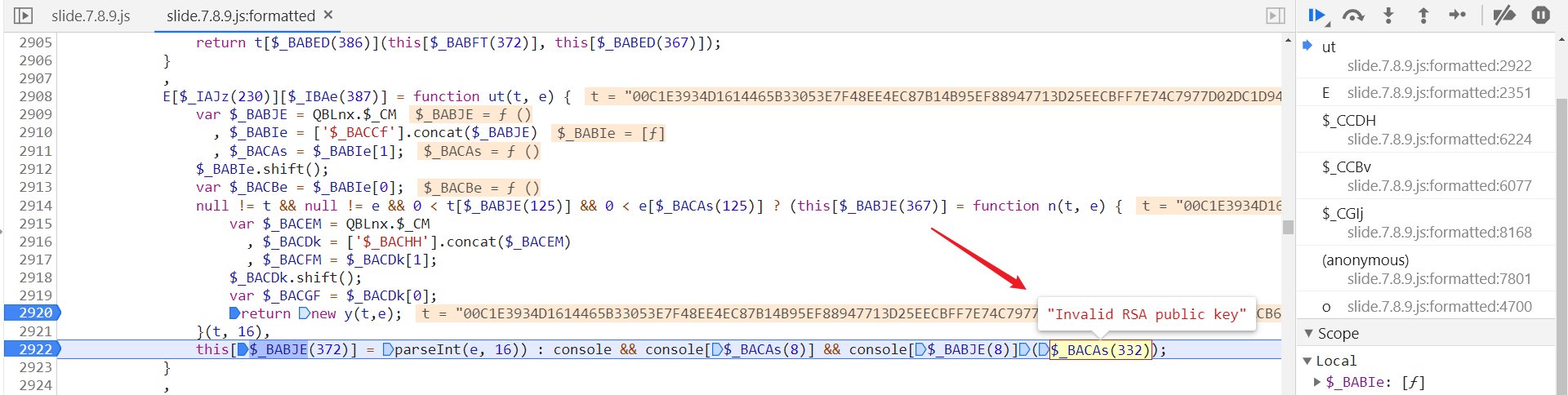
第 2908 行,ut 函数传入了两个值,t 为公钥值,e 为公钥模数,都是固定值:
这里可以直接引库复现,也可以选择将算法部分扣下来,局部搜索 var U = function,在第 2043 行,将整个自执行函数扣下来,这里随机数后期写成固定值,后面也有随机数,不然会造成传参不匹配:
var U = function () {
// 此处过长,省略
}();
// 随机数, 一组四个数
function t() {
random_str = (65536 * (1 + Math["random"]()) | 0)["toString"](16)["substring"](1);
return random_str;
}
// 随机数, 四个数一组, 四组
function getRandomStr() {
return t() + t() + t() + t();
}
// u 值
var u = new U()['encrypt'](getRandomStr());
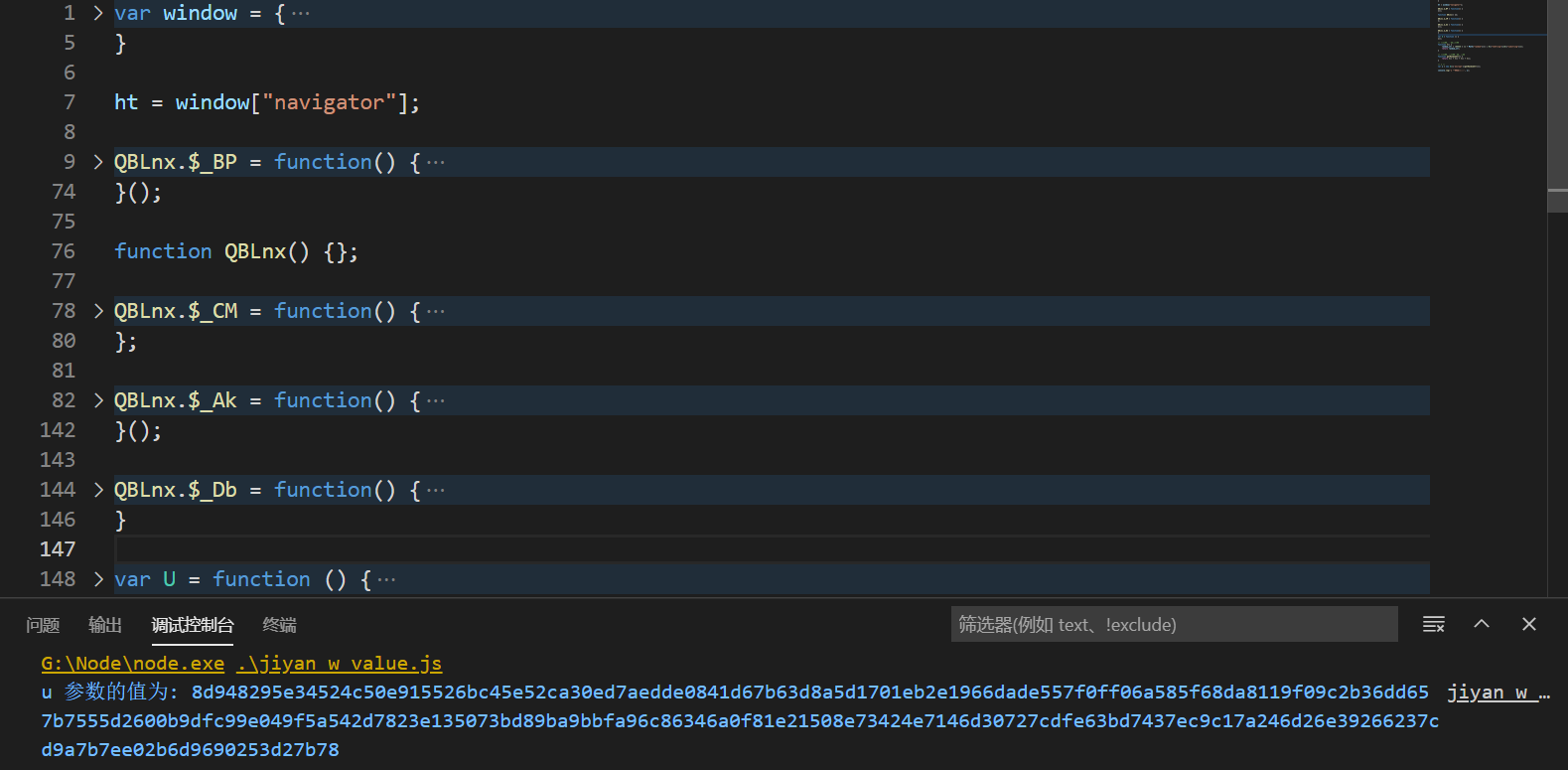
console.log('u 参数的值为:', u);
运行后报错提示,QBLnx is not defined:

其定义在第 136 行,是个函数对象,补上即可:
function QBLnx() {};
运行后报错提示,$_IBAe is not a function:

搜索后可知,其定义在第 128 行:
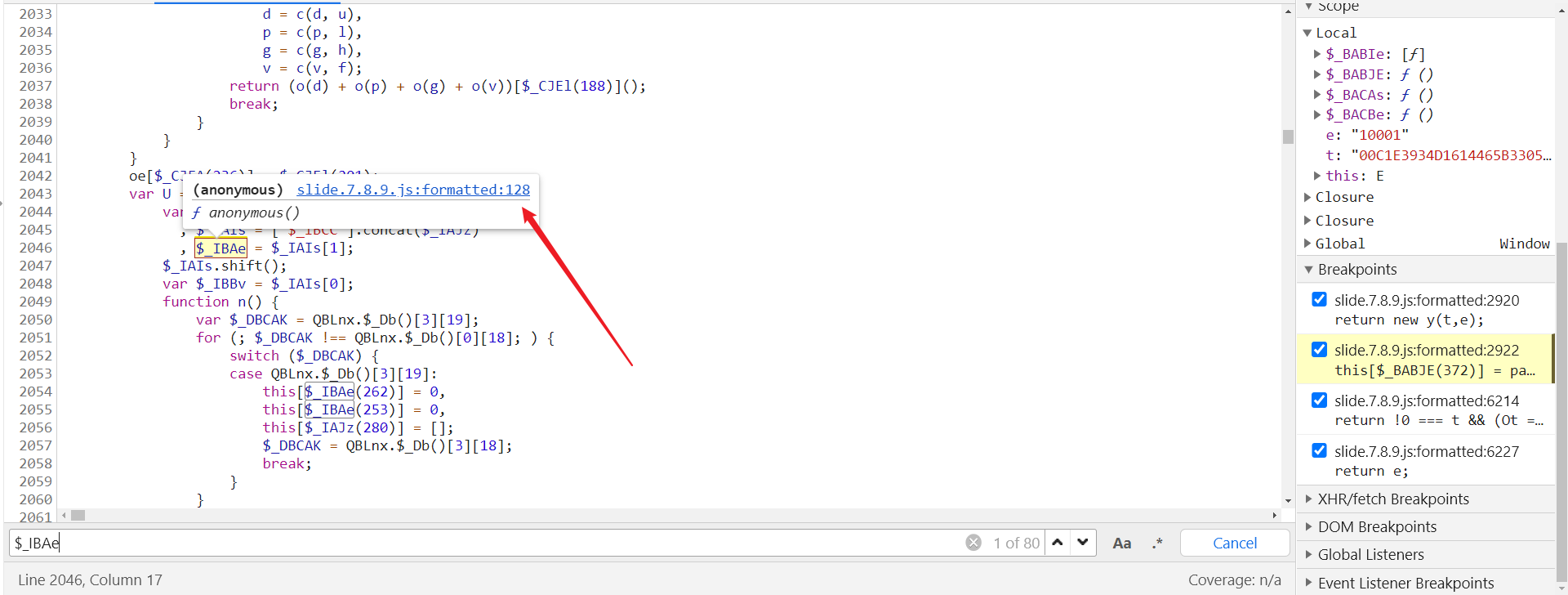
跟进过去将该部分扣下来:
QBLnx.$_CM = function() {
return typeof QBLnx.$_Ak.$_DBGGT === 'function' ? QBLnx.$_Ak.$_DBGGT.apply(QBLnx.$_Ak, arguments) : QBLnx.$_Ak.$_DBGGT;
};
接着报错提示,Cannot read property '$_DBGGT' of undefined:

定义在第 7 行,直接将 QBLnx.$_Ak 整个扣下来即可,然后会报错提示,window 和 ht 未定义,ht 为 navigator:
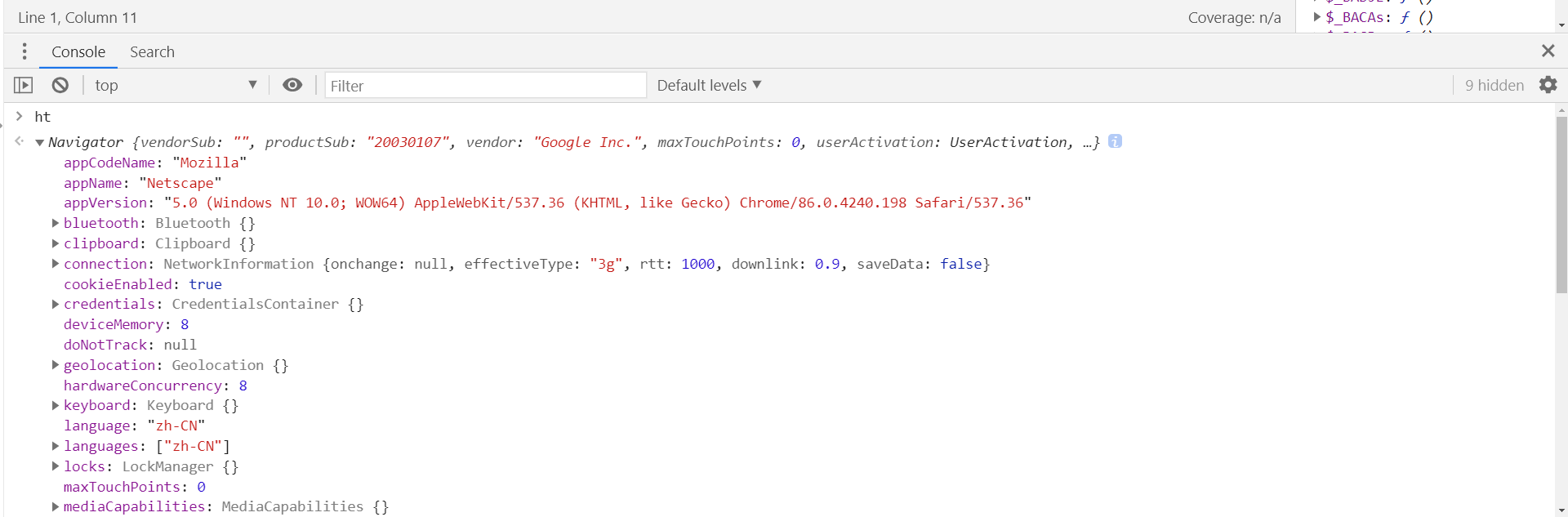
var window = {
"navigator": {
"appName": "Netscape",
},
}
ht = window["navigator"];
又报错提示,QBLnx.$_Db is not a function:

其定义在第 132 行,扣下来补上:
QBLnx.$_Db = function() {
return typeof QBLnx.$_BP.$_DBHGJ === 'function' ? QBLnx.$_BP.$_DBHGJ.apply(QBLnx.$_BP, arguments) : QBLnx.$_BP.$_DBHGJ;
};
报错提示,Cannot read property '$_DBHGJ' of undefined:

通过搜索,其定义在第 68 行,将 QBLnx.$_BP 整个扣下来即可,至此,u 参数成功复现:
l 参数
u 参数解决后,接着需要分析 l 参数,内容如下:
// 混淆
l = V[$_CAIAt(353)](gt[$_CAIAt(218)](o), r[$_CAIAt(756)]());
// 未混淆
l = V["encrypt"](gt["stringify"](o), r["$_CCEc"]());
可以知道,l 参数的结果是将 gt["stringify"](o) 和 r["$_CCEc"]() 加密后得到的,先来分析 r["$_CCEc"]() ,选中后跟进进去,跳转到了熟悉的第 6208 行,就是之前的 16 位随机字符串:

将这里写成跟之前一样的固定值, gt["stringify"](o) 返回的是 JSON 格式的数据,由 o 参数生成:

对比分析以下 o 参数中,哪些是定值,哪些是动态变化的,可以看到箭头所指的值都不一样了:
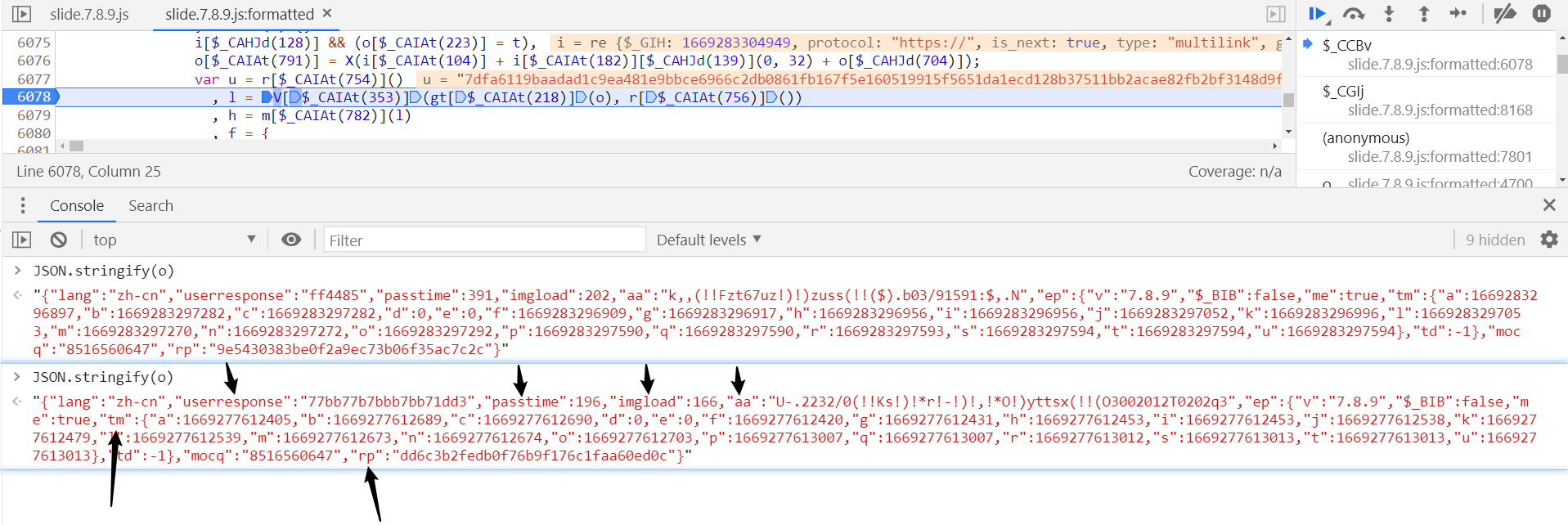
接下来对关键值进行分析,先来分析下 userresponse,o 定义在第 6012 行:
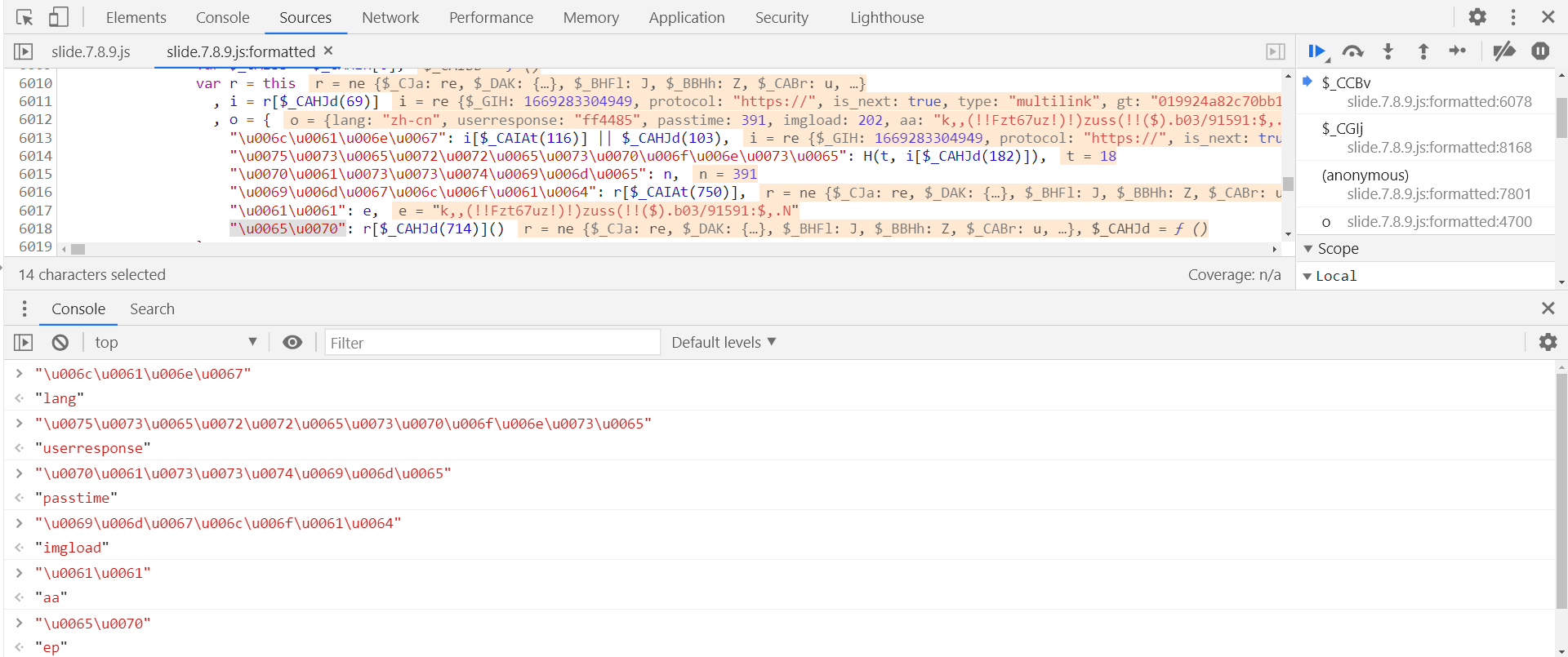
var o = {
"lang": i[$_CAIAt(116)] || $_CAHJd(103),
"userresponse": H(t, i[$_CAHJd(182)]),
"passtime": n,
"imgload": r[$_CAIAt(750)],
"aa": e,
"ep": r[$_CAHJd(714)]()
};
userresponse 定义在第 6014 行,需要分析 H(t, i[$_CAHJd(182)]),控制台打印一下:
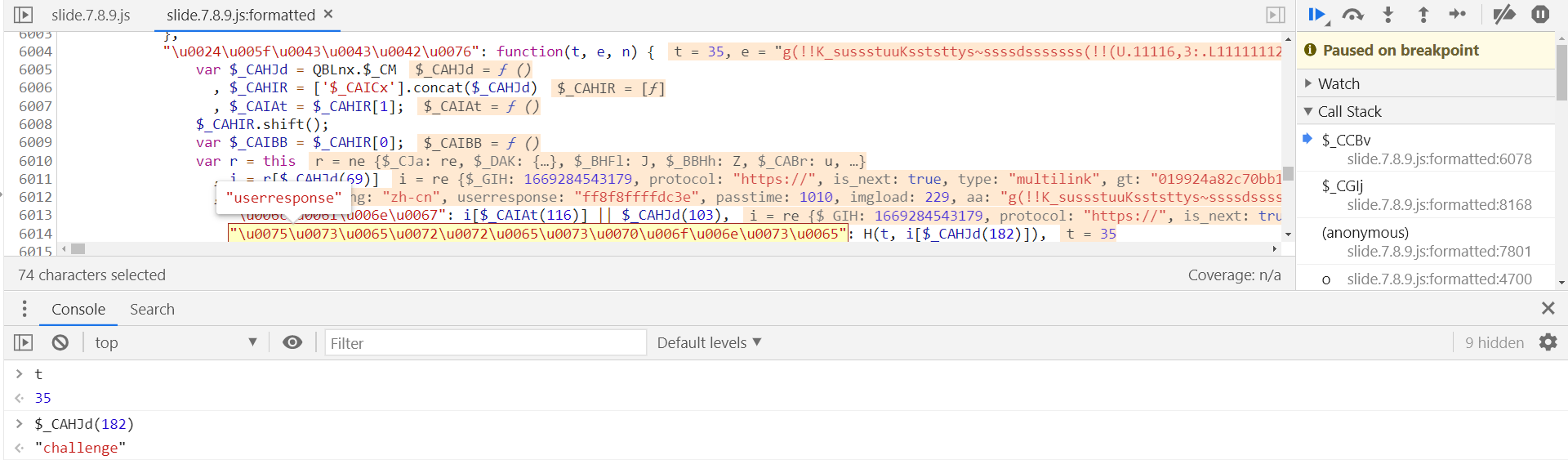
t 为滑动滑块的距离,需要注意的是 i[$_CAHJd(182)] 为第二个 ajax.php?xxx 传递的 challenge,比注册请求时的 challenge 长两位,再将 H 参数扣下来即可,其定义在第 704 行,报错提示,$_CJFA is not defined:

定义在第 159 行:
var $_CJEl = QBLnx.$_CM
, $_CJDa = ['$_CJHo'].concat($_CJEl)
, $_CJFA = $_CJDa[1];
至此,userresponse 成功复现,接下来看 passtime,n 值此时已经生成了,为 1010,向上跟栈到 $_CGlj 中:
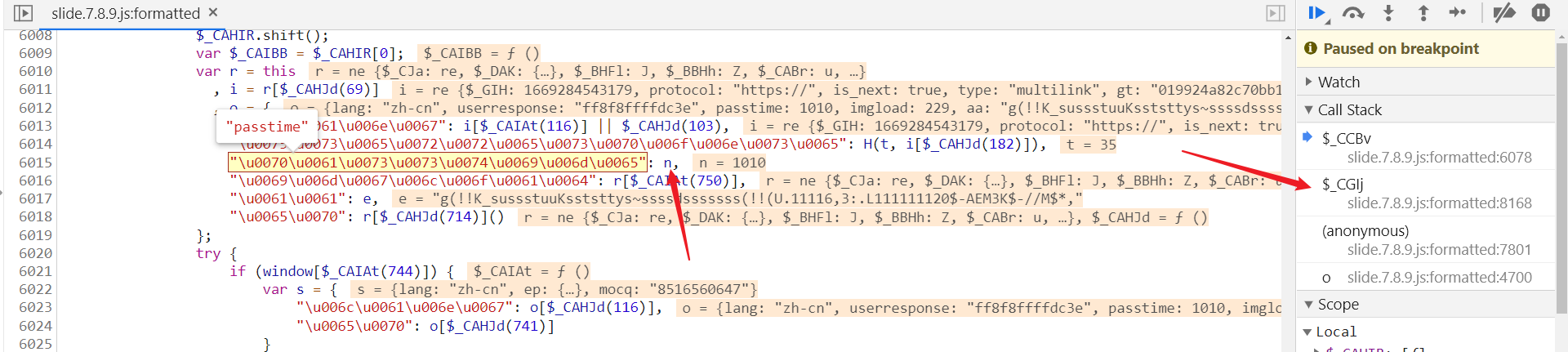
n[$_DAAAV(871)] 为 passtime 值,定义在第 8164 行,为滑动结束时间 - 开始时间:
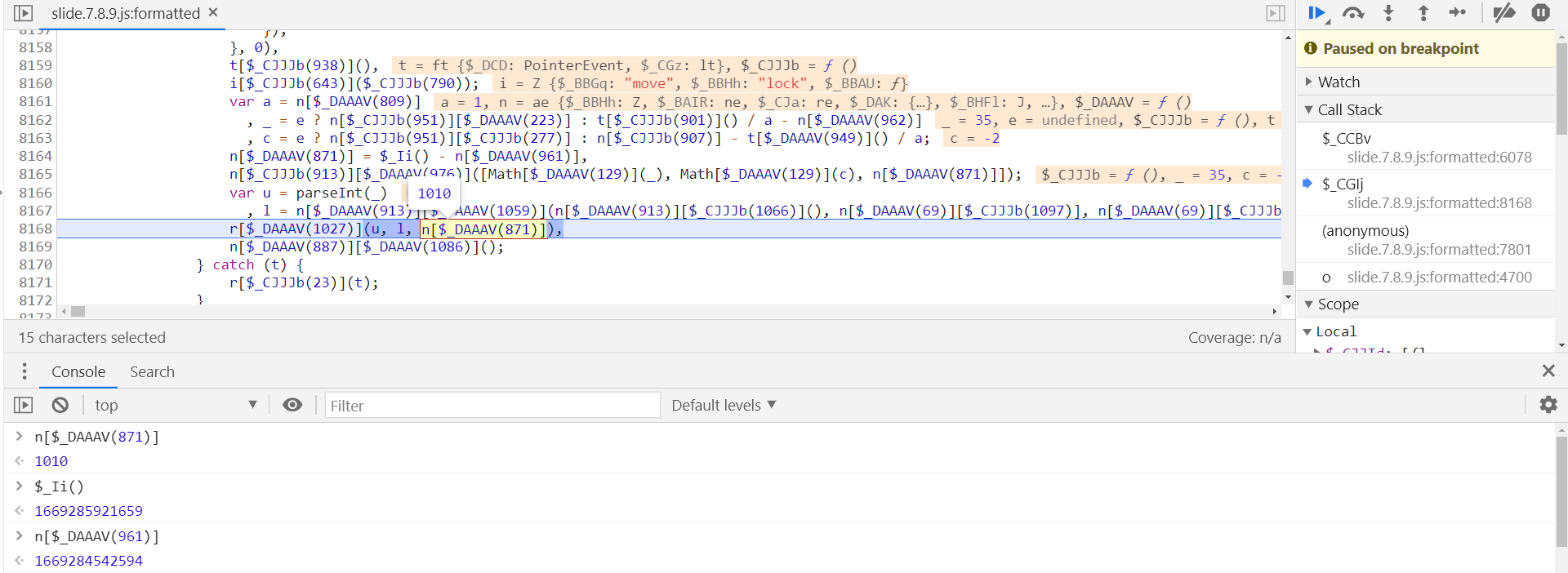
接下来分析下 aa 参数,其定义在第 6017 行,值由参数 e 传递,同样向上跟栈到 $_CGlj 中,为第 8168 行的 l 值,l 定义在第 8167 行,三个参数加密后得到:
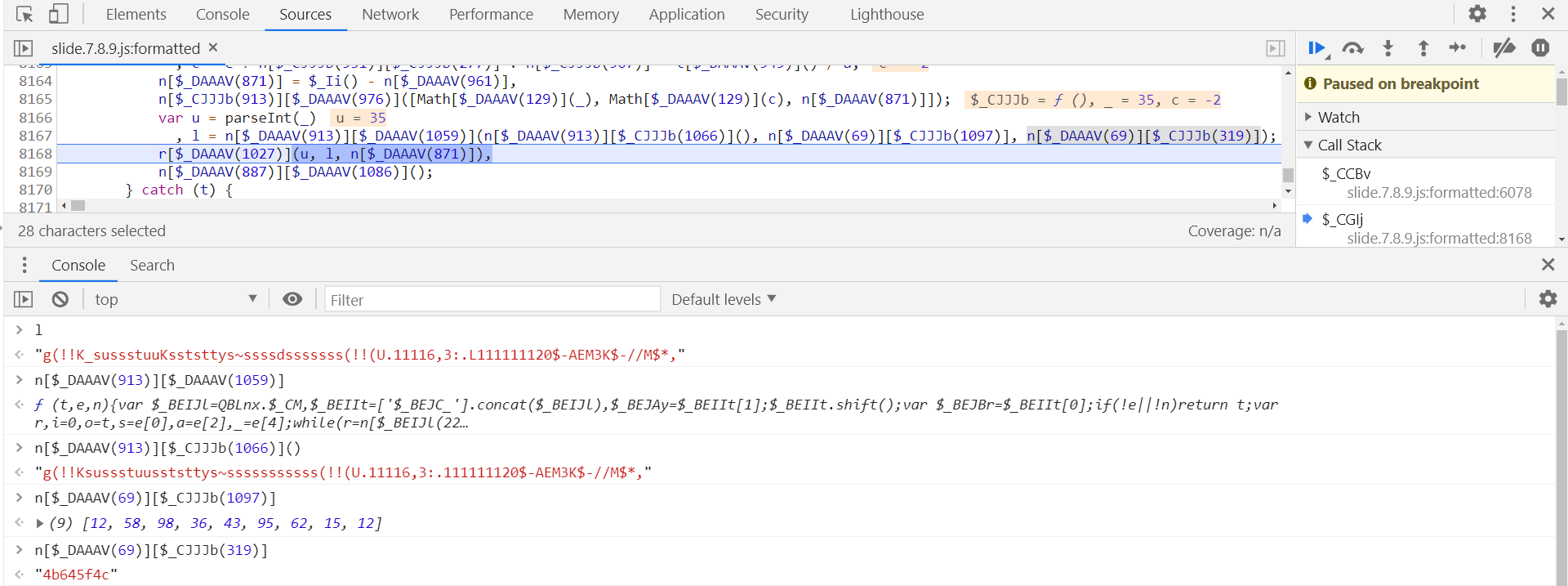
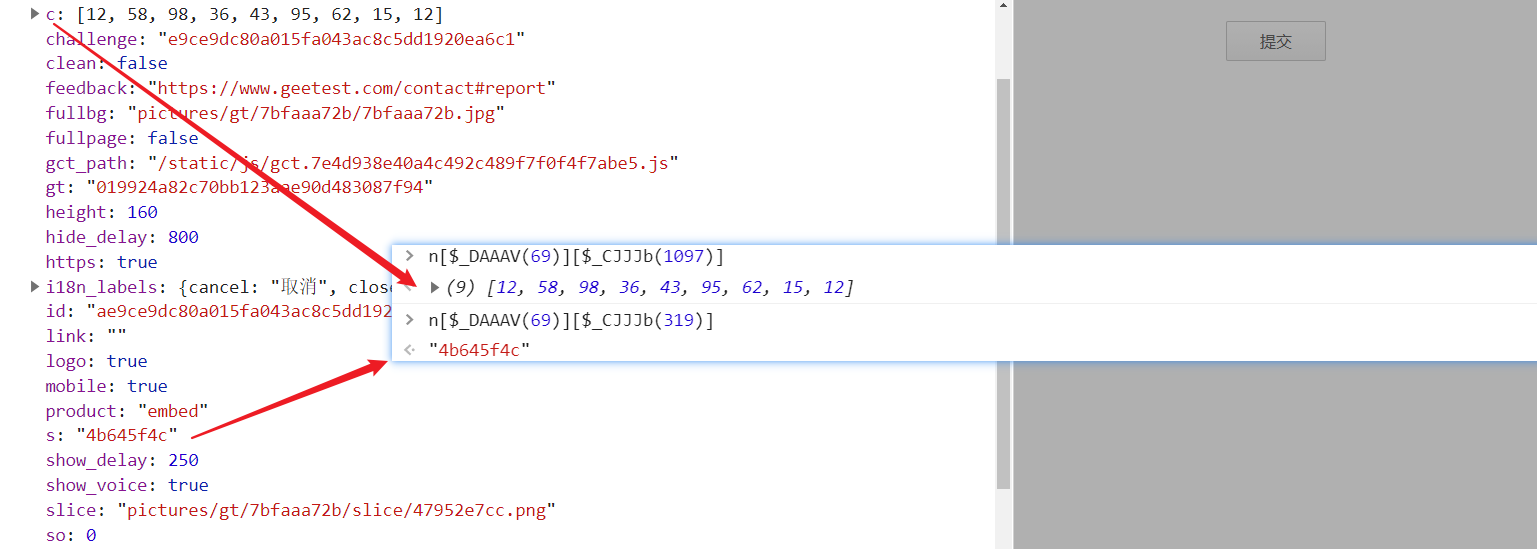
接下来跟进到 n[$_DAAAV(913)][$_CJJJb(1066)] 中,分析下轨迹是如何加密的,在第 4065 行,于第 4133 行打下断点,第 4108 行的 this[$_BEHAL(343)] 即为轨迹值,关于轨迹算法后面会专门出一期文章:
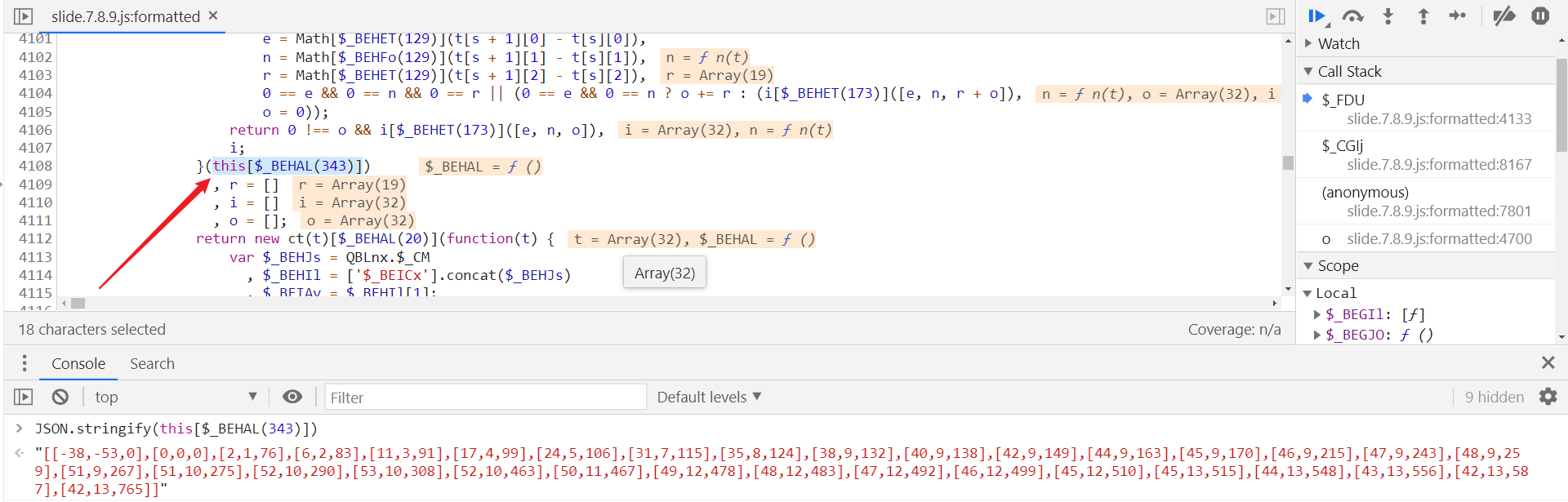
将整个算法部分抠出来,先将轨迹值固定,写成参数传递进去,不然会报错提示,Cannot read property 'length' of undefined,因为轨迹值是别的算法生成的,不传值即为空,运行程序,会报错提示,ct is not defined:

ct 定义在第 4223 行,扣下来,报错提示,(intermediate value)[$_BEHAL(...)] is not a function:

定义在第 4326 行,补上以下内容,即可复现:
ct["prototype"] = {
"\u0024\u005f\u0043\u0041\u0051": function(t) {
var $_BFFJi = QBLnx.$_CM
, $_BFFIX = ['$_BFGCq'].concat($_BFFJi)
, $_BFGAT = $_BFFIX[1];
$_BFFIX.shift();
var $_BFGBV = $_BFFIX[0];
var e = this[$_BFFJi(461)];
if (e[$_BFGAT(419)])
return new ct(e[$_BFFJi(419)](t));
for (var n = [], r = 0, i = e[$_BFGAT(125)]; r
结果对比一致:
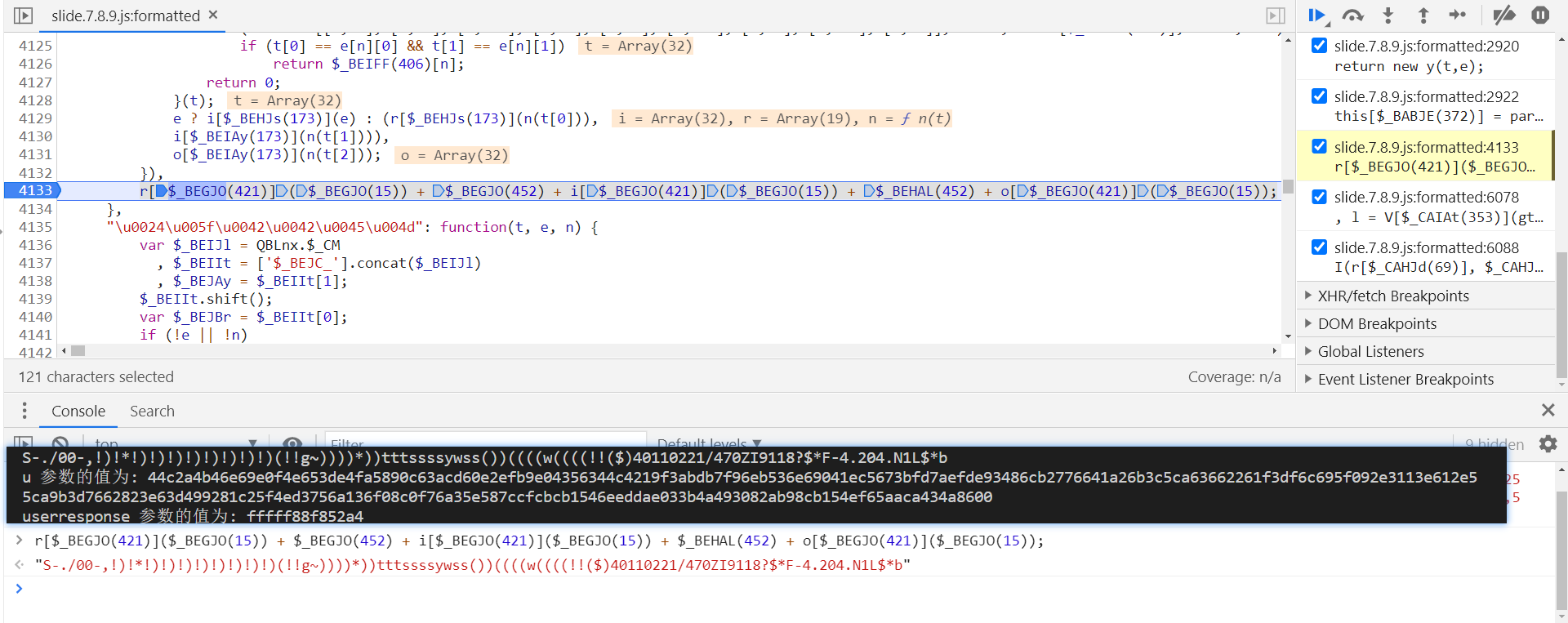
后面三个参数的值都分析完了,回到第 8167 行 l 处,跟进到 n[$_DAAAV(913)][$_DAAAV(1059)] 中,在第 4135 行,扣下来即可:
function getAA(t, e, n) {
var $_BEIJl = QBLnx.$_CM
, $_BEIIt = ['$_BEJC_'].concat($_BEIJl)
, $_BEJAy = $_BEIIt[1];
$_BEIIt.shift();
var $_BEJBr = $_BEIIt[0];
if (!e || !n)
return t;
var r, i = 0, o = t, s = e[0], a = e[2], _ = e[4];
while (r = n[$_BEIJl(229)](i, 2)) {
i += 2;
var c = parseInt(r, 16)
, u = String[$_BEJAy(237)](c)
, l = (s * c * c + a * c + _) % t[$_BEJAy(125)];
o = o[$_BEJAy(229)](0, l) + u + o[$_BEJAy(229)](l);
}
return o;
};
将 c 和 s 写为固定值,对比结果一致:
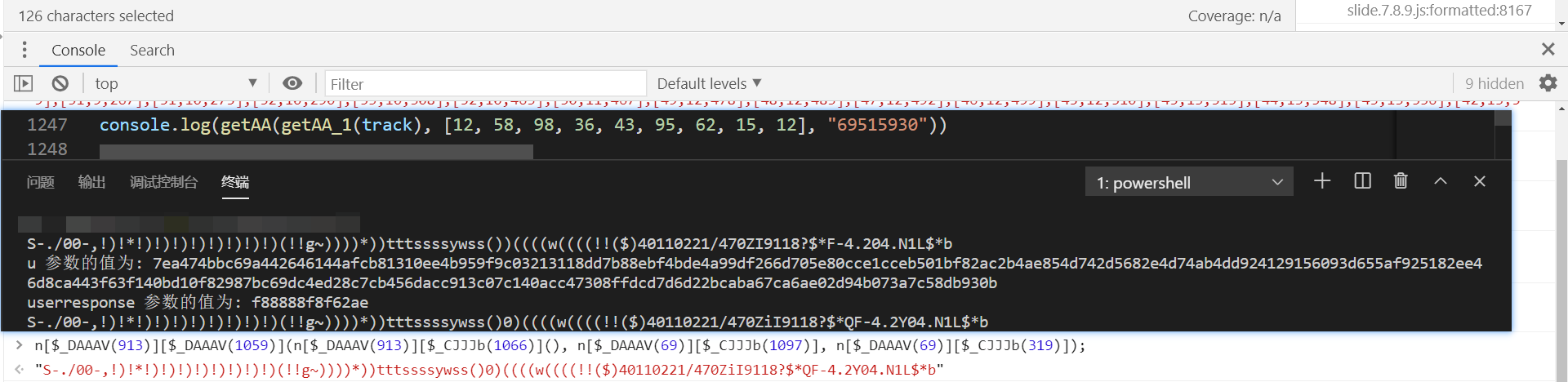
aa 参数分析完成,接下来分析 rp 参数,定义在第 6076 行:
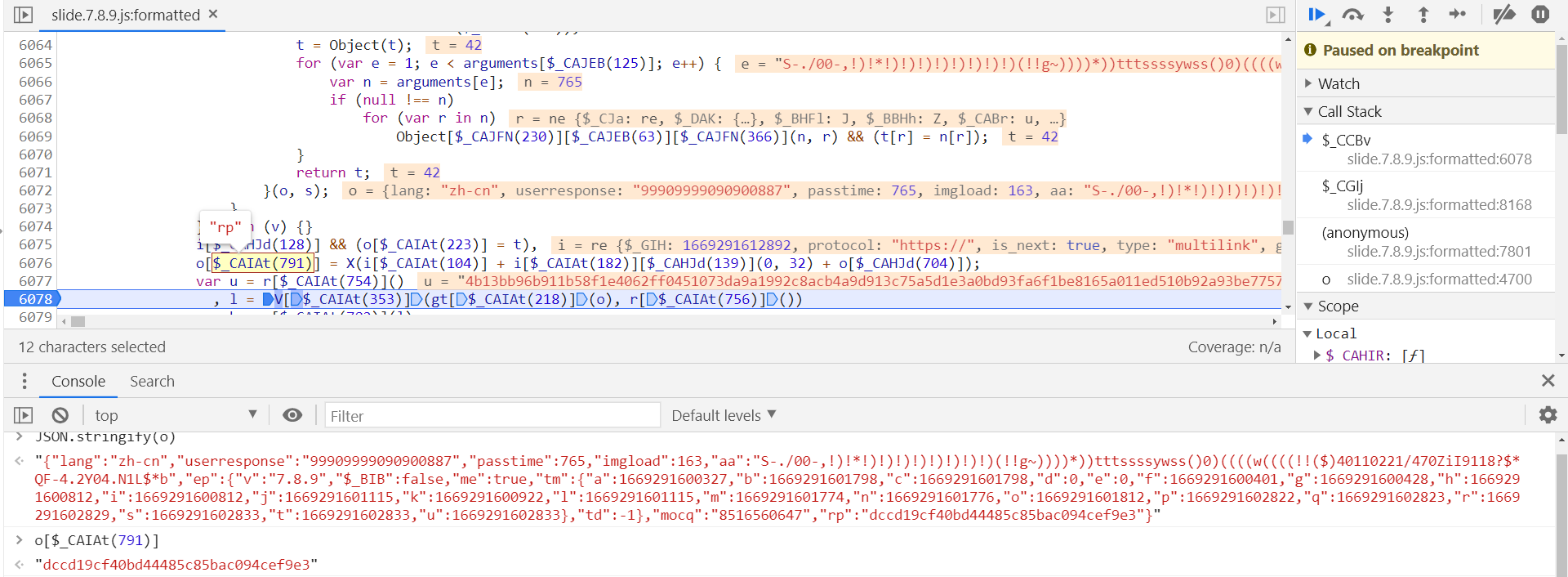
// 混淆
o[$_CAIAt(791)] = X(i[$_CAIAt(104)] + i[$_CAIAt(182)][$_CAHJd(139)](0, 32) + o[$_CAHJd(704)]);
// 未混淆
o["rp"] = X(i["gt"] + i["challenge"]["slice"](0, 32) + o["passtime"]);
后面三个参数都很明显了,跟进到 X 函数中,在第 1876 行,扣下来即可,对比结果一致:
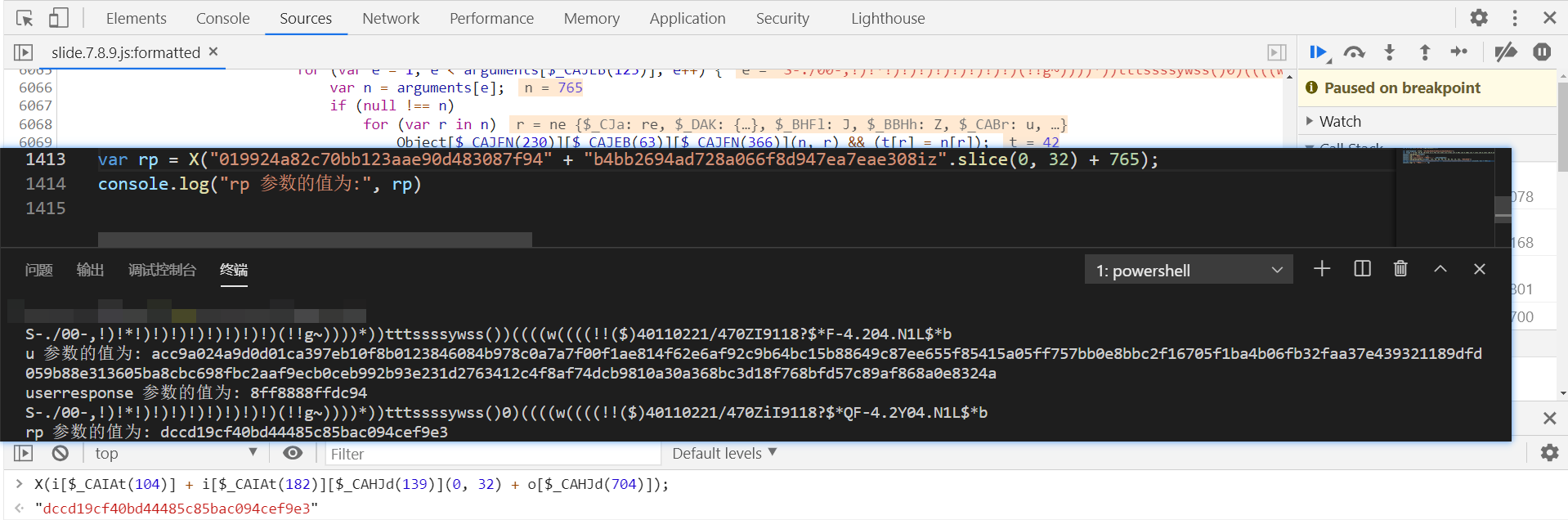
这里是 MD5 加密,也可以直接通过引库复现:
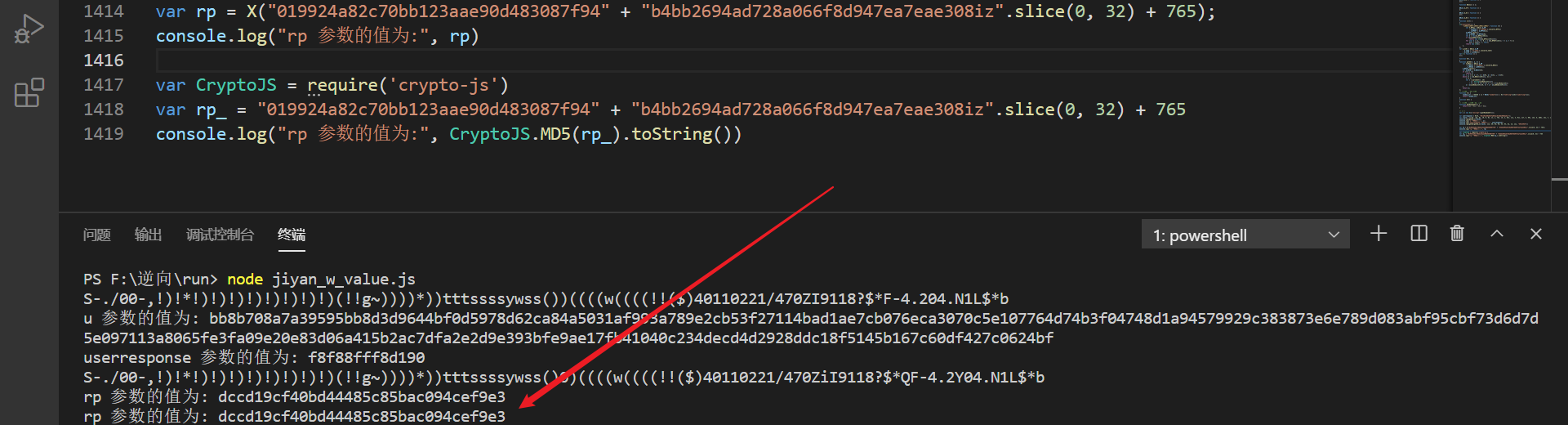
ep 定义在第 6018 行,跟进到 r[$_CAHJd(714)] 中,tm 参数定义在第 6239 行:
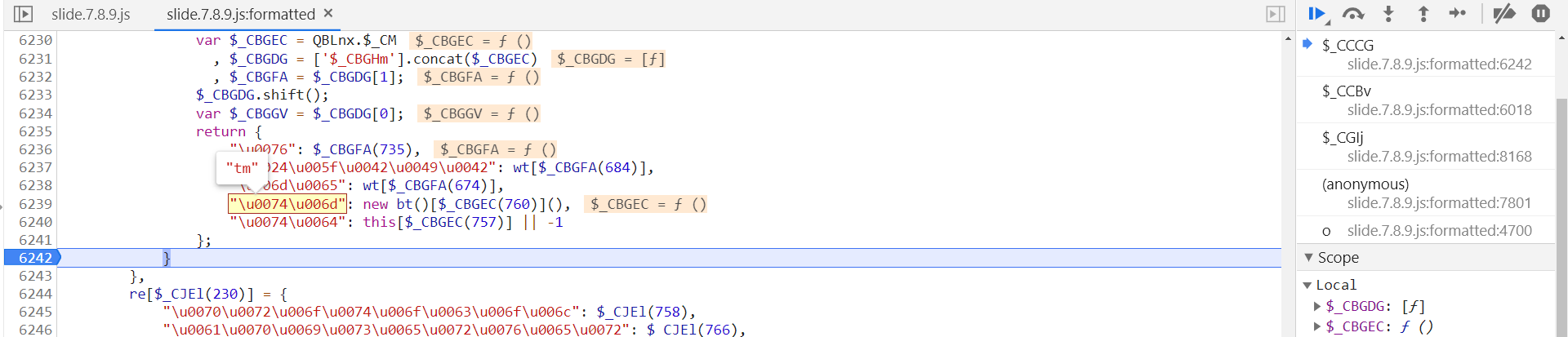
跟进 new bt()[$_CBGEC(760)] 中,在第 5268 行打下断点,tm 结果如下:
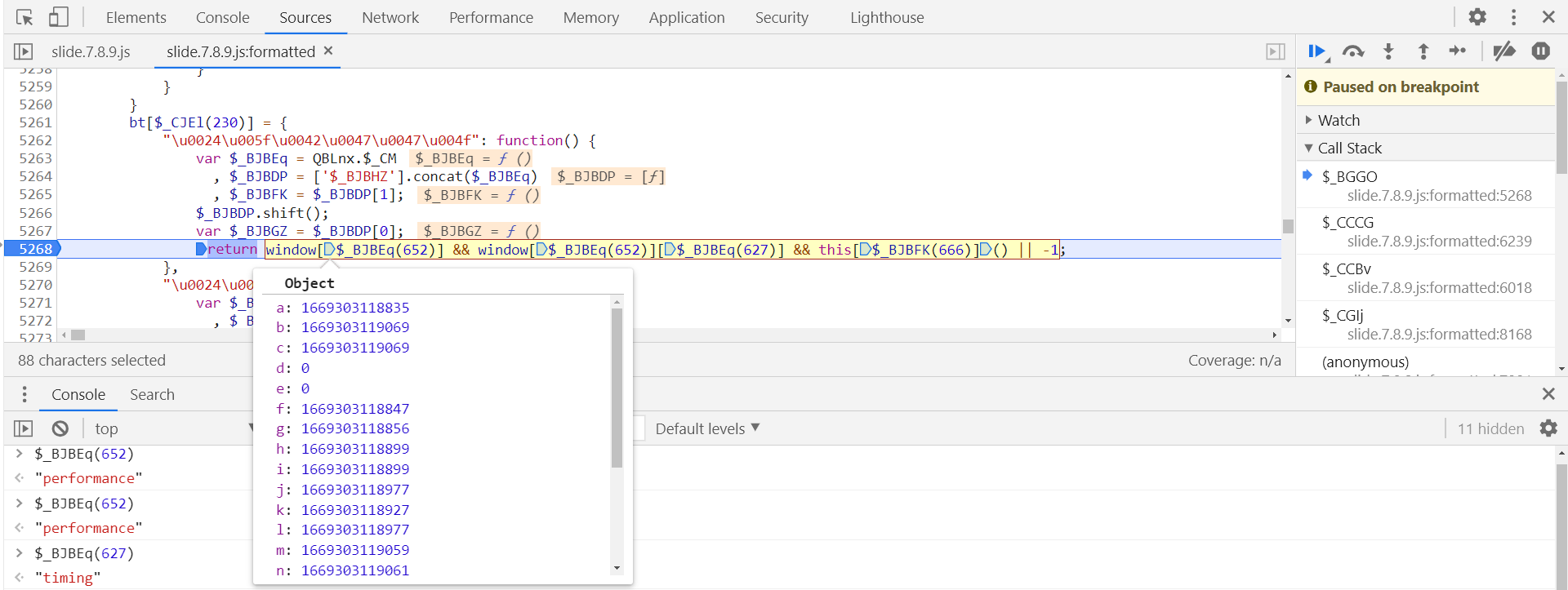
至此,参数 o 复现完毕,回到第 6078 行,分析完 V[$_CAIAt(353)] l 即完成,跟进,定义在第 3218 行,在第 3230 行打下断点,这里为 AES 加密,初始向量 iv 值为 "0000000000000000":
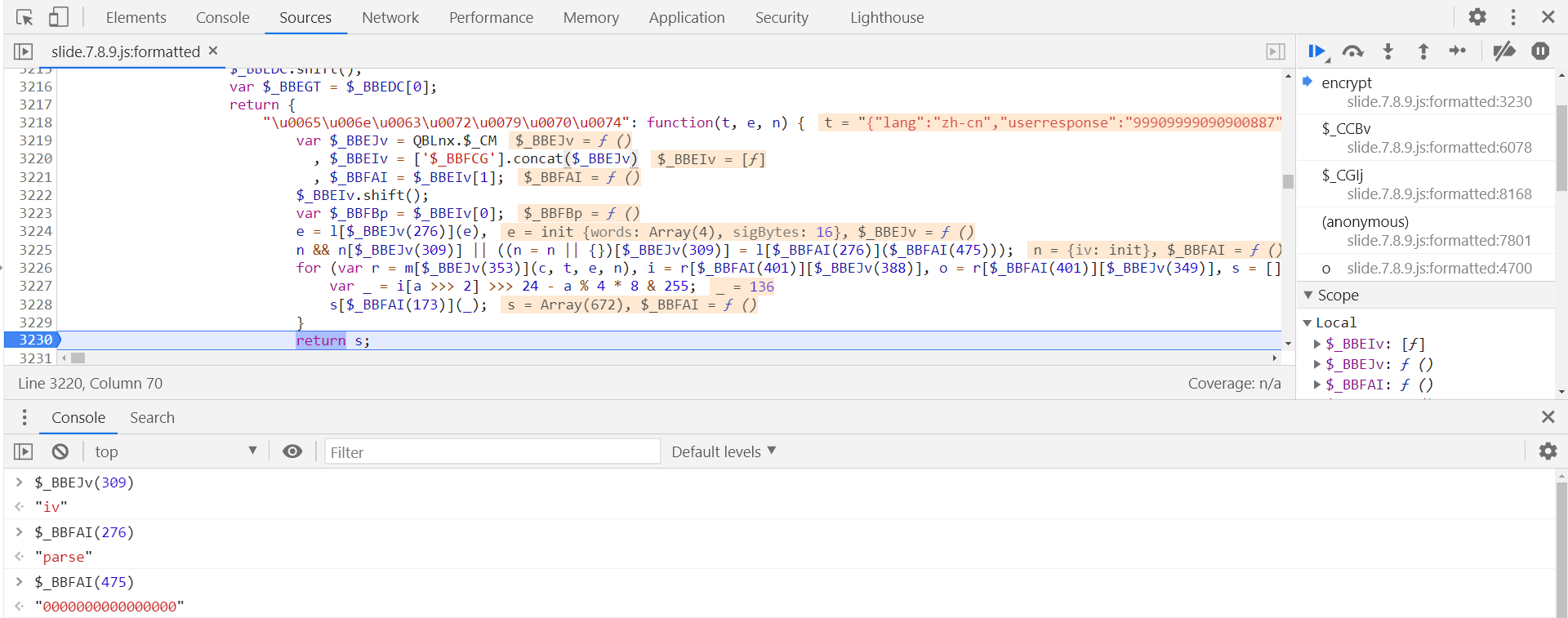
直接引库复现:
function aesV(o_text, random_str) {
var key = CryptoJS.enc.Utf8.parse(random_str);
var iv = CryptoJS.enc.Utf8.parse("0000000000000000");
var srcs = CryptoJS.enc.Utf8.parse(o_text);
var encrypted = CryptoJS.AES.encrypt(srcs, key, {
iv: iv,
mode: CryptoJS.mode.CBC,
padding: CryptoJS.pad.Pkcs7
});
for (var r = encrypted, o = r.ciphertext.words, i = r.ciphertext.sigBytes, s = [], a = 0; a >> 2] >>> 24 - a % 4 * 8 & 255;
s.push(c);
}
return s;
};
对比结果一致:
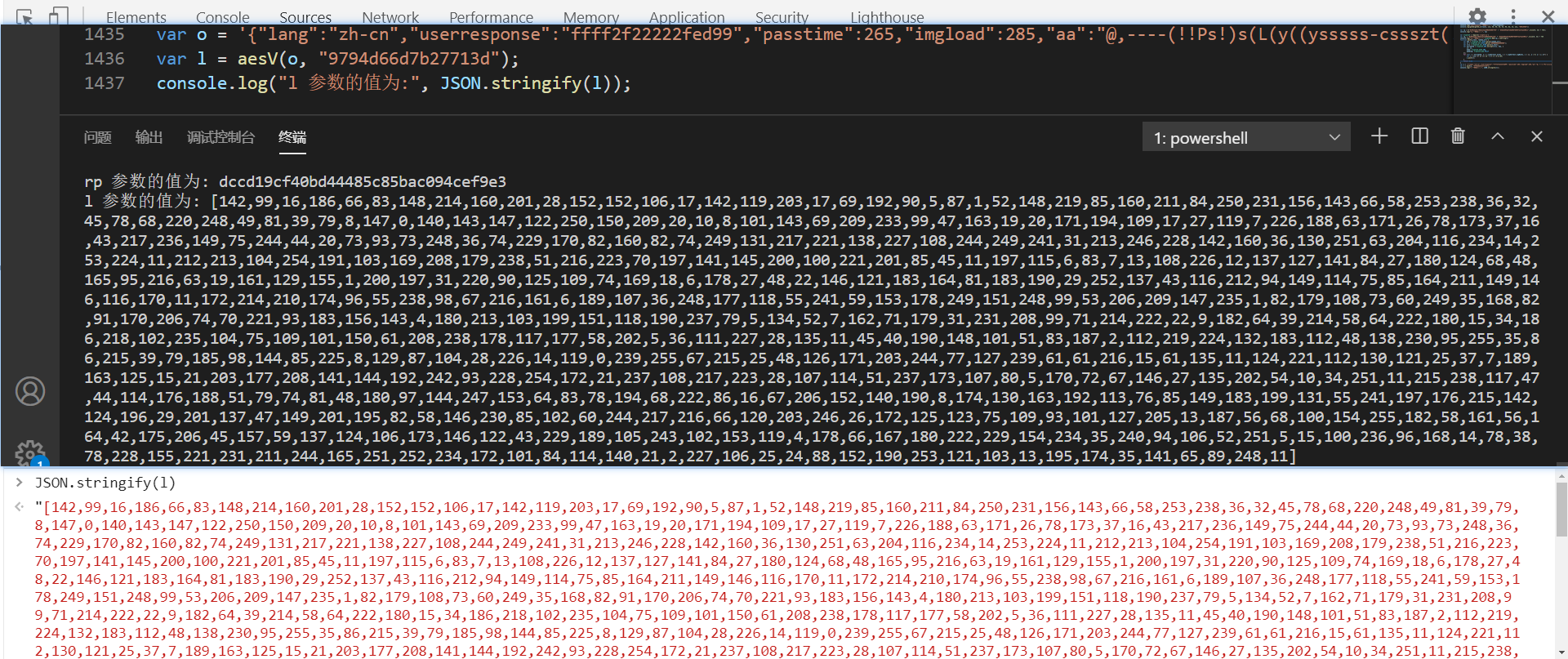
l 参数分析完毕,终于只剩下一个 h 了,m[$_CAIAt(782)](l) 即将 l 加密后得到的,跟进 m[$_CAIAt(782)],定义在第 1568 行,在第 1575 行打下断点,为 e 中两个 value 值相加:
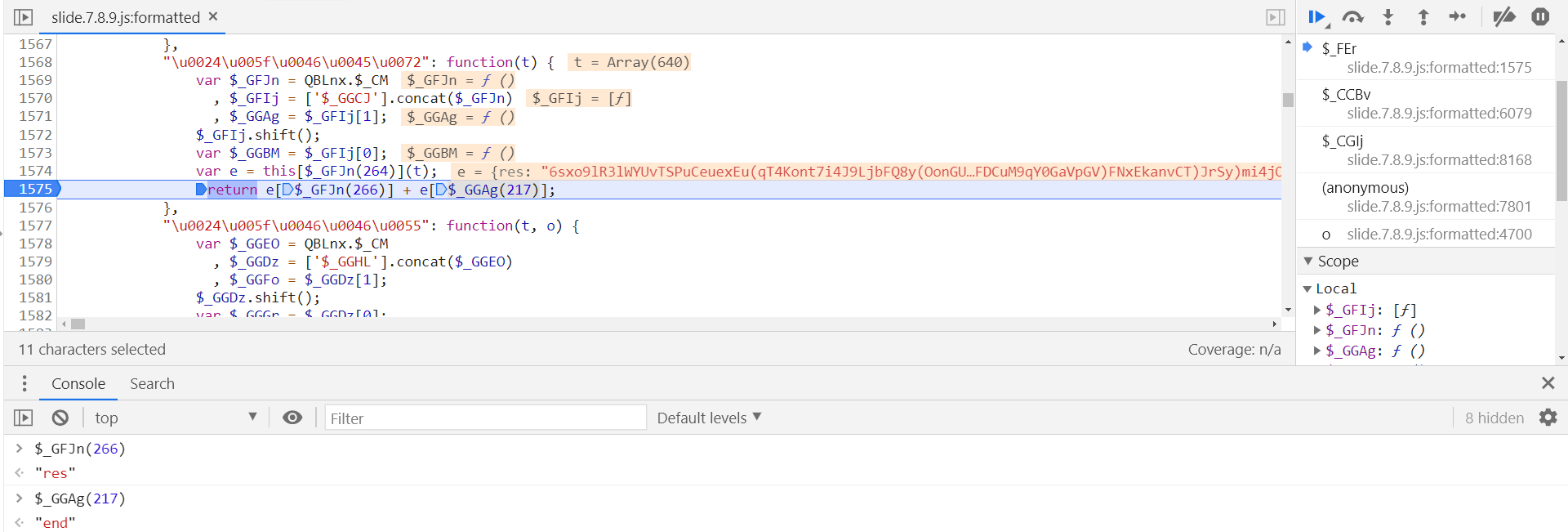
e 定义在第 1574 行,t 为传入的 l 参数,跟进到 this[$_GFJn(264)] 中,在第 1523 行,复现如下:
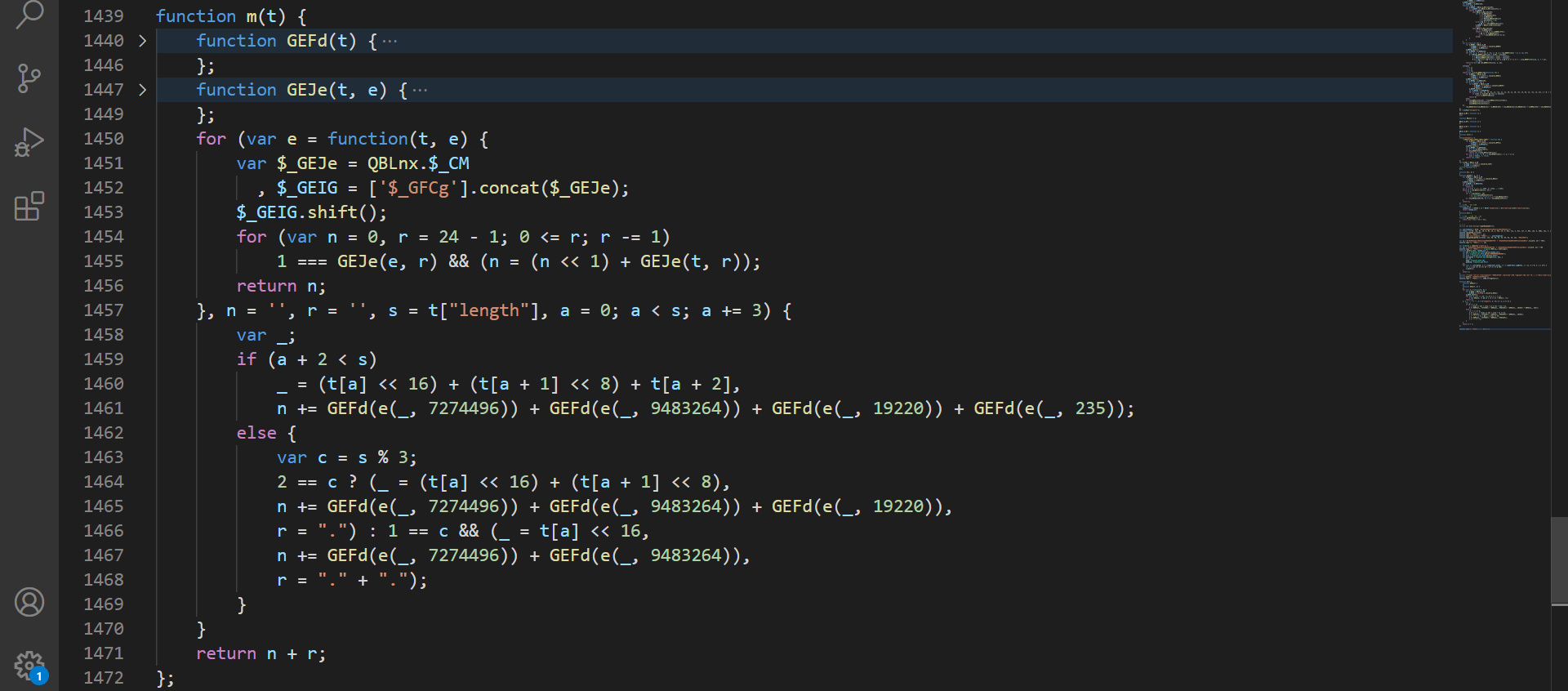
校验结果一致:
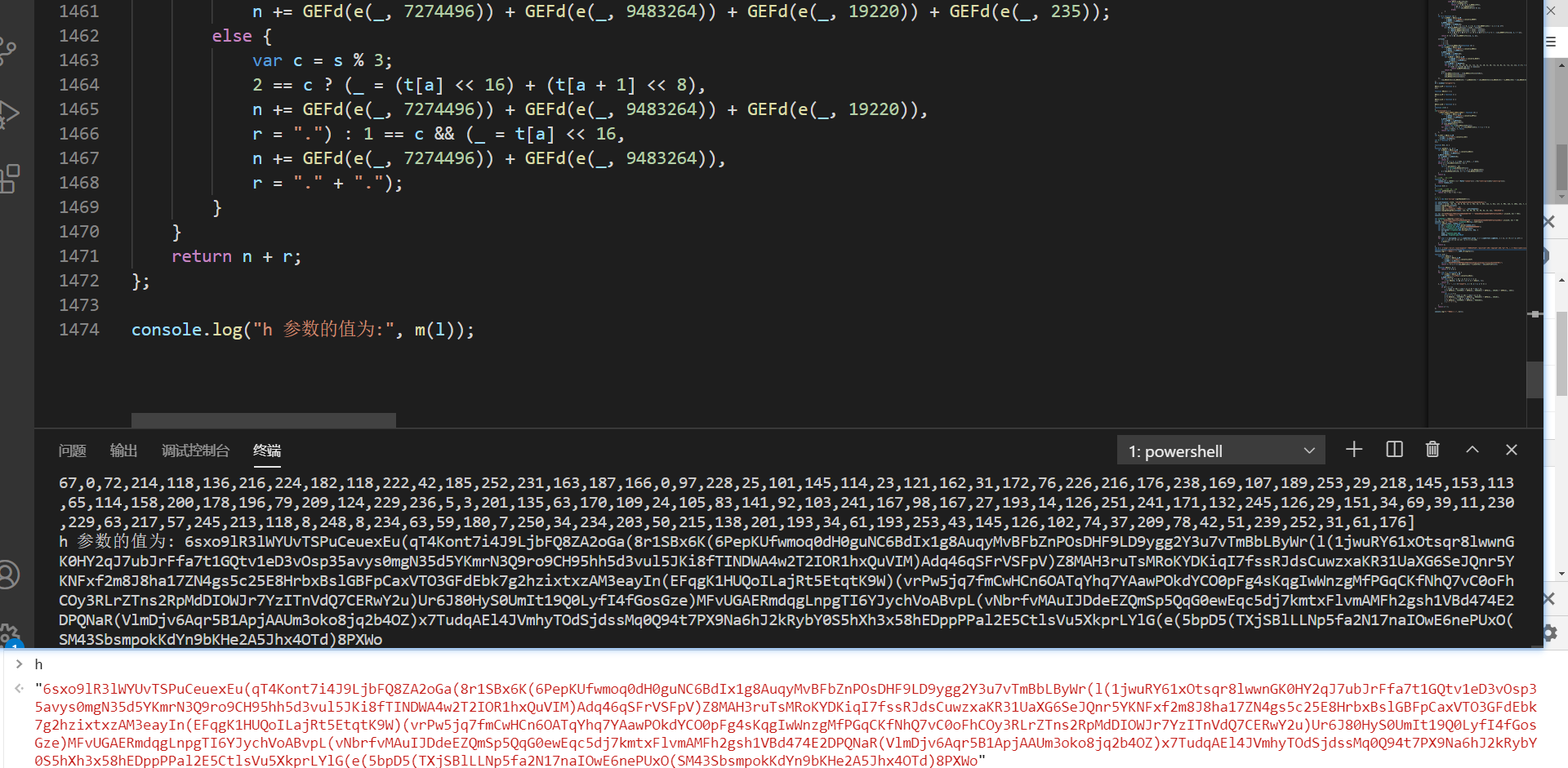
w 参数至此终于全部复现完成!
底图还原
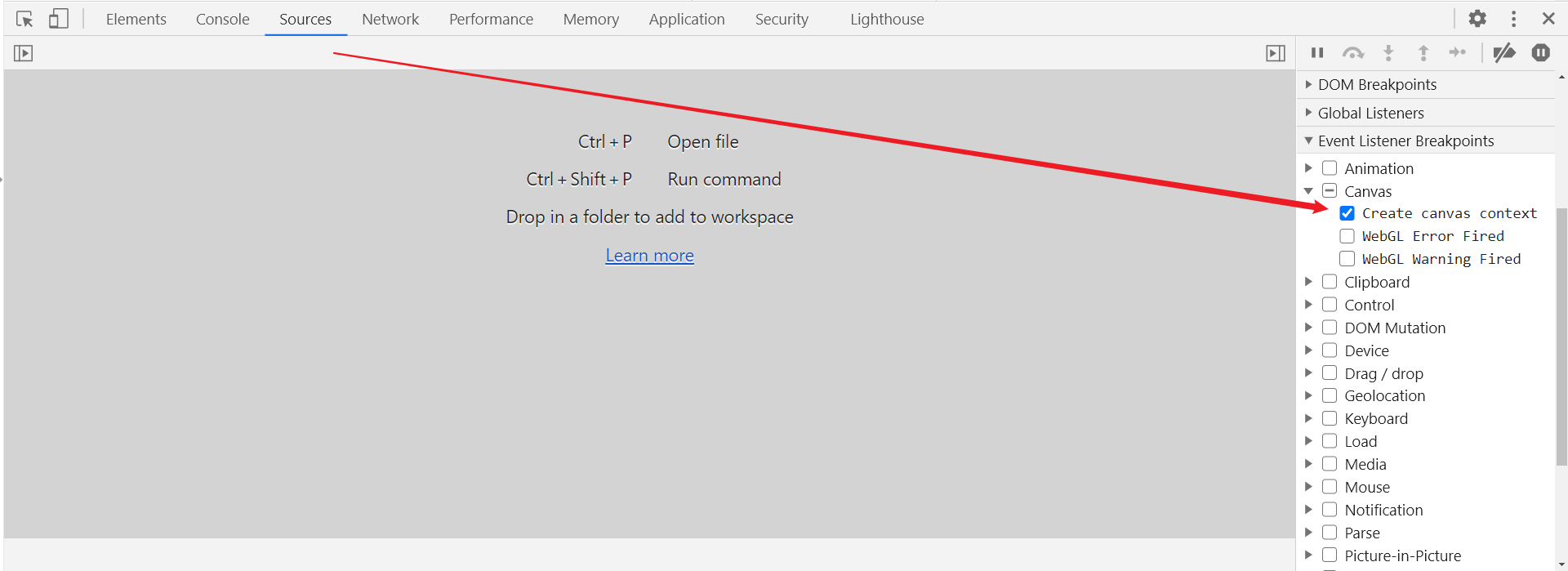
前文说过,拿到的完整背景图以及带缺口背景图都是被打乱了的,这里需要还原才能计算滑动距离以及轨迹等,极验的底图是通过 Canvas 绘制出来的,直接打下事件断点:
点击按钮进行验证即会断住,格式化后跳转到第 295 行,
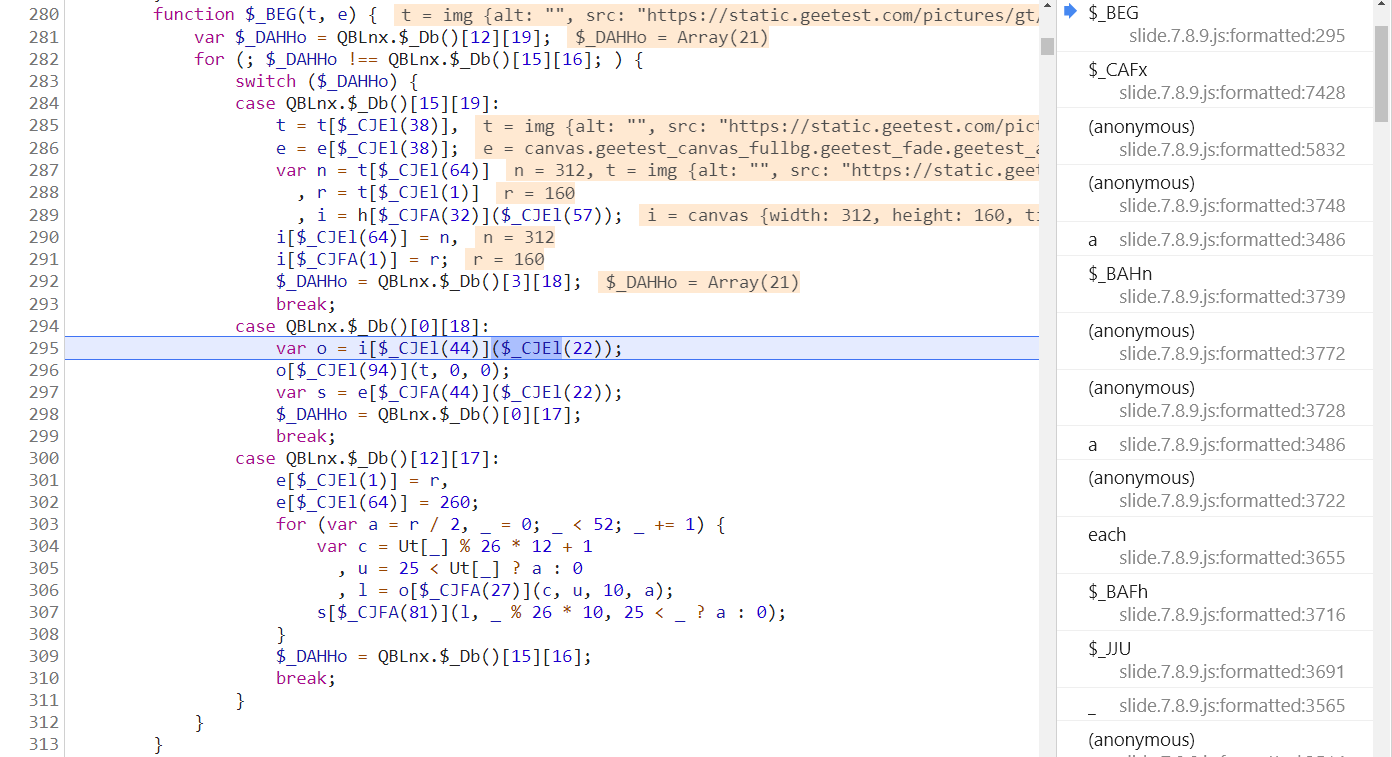
简单解一波混淆,会清晰一些:
function $_BEG(t, e) {
var $_DAHHo = QBLnx.$_Db()[12][19];
for (; $_DAHHo !== QBLnx.$_Db()[15][16];) {
switch ($_DAHHo) {
case QBLnx.$_Db()[15][19]:
t = t["$_CGz"],
e = e["$_CGz"];
var n = t["width"]
, r = t["height"]
, i = h["createElement"]("canvas");
i["width"] = n,
i["height"] = r;
$_DAHHo = QBLnx.$_Db()[3][18];
break;
case QBLnx.$_Db()[0][18]:
var o = i["getContext"]("2d");
o["drawImage"](t, 0, 0);
var s = e["getContext"]("2d");
$_DAHHo = QBLnx.$_Db()[0][17];
break;
case QBLnx.$_Db()[12][17]:
e["height"] = 160,
e["width"] = 260;
for (var a = r / 2, _ = 0; _
控制流平坦化混淆,可以通过 AST 技术解混淆,AST 相关可以看 K 哥往期文章:逆向进阶,利用 AST 技术还原 JavaScript 混淆代码,这里就不对此进行讲解了,这里就是 Canvas 绘图的过程,关键乱序算法部分在 QBLnx.$_Db()[12][17] 中:
e["height"] = 160,
e["width"] = 260;
for (var a = r / 2, _ = 0; _
原图比例为 312 x 160,宽为 320,长为 160:
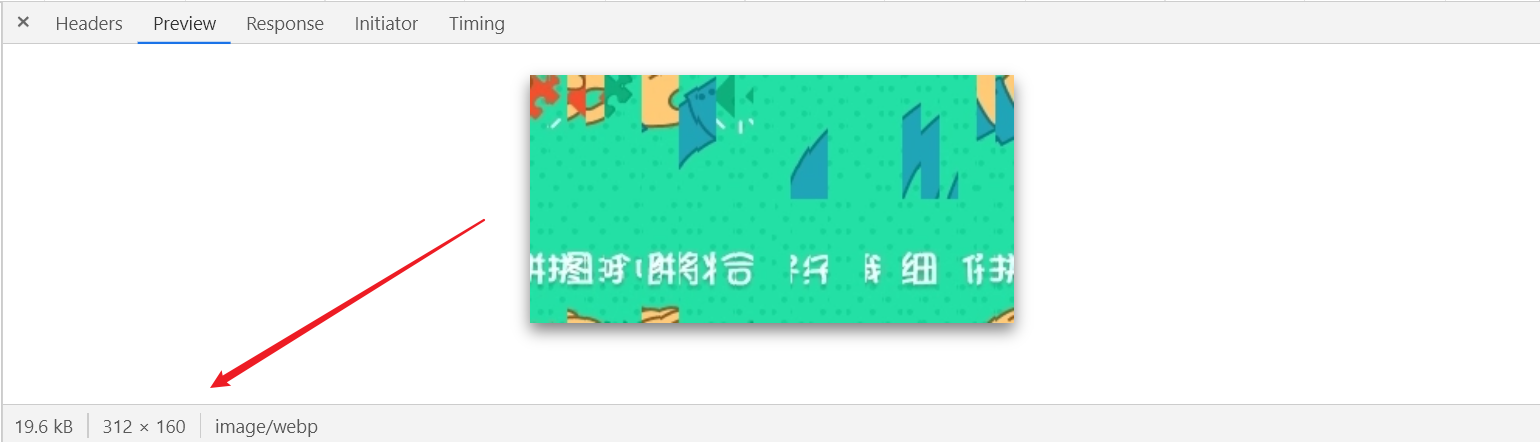
e["height"] = 160、e["width"] = 260 指还原后的图片比例为 260 x 160,a 的值为 r / 2 即 80,就是将整张图片分为了上下两等分,再将图片纵向切割为了 26 等份,Ut 数组的长度为 52,Ut[] 即依次取数组中的元素,Ut 数组即为图片还原的顺序,是固定的,`25 ] ? a : 0 判断图片是上半部分还是下半部分,_ % 26 * 10` 表示每个小块取 10 px 像素,正确图片的顺序为:
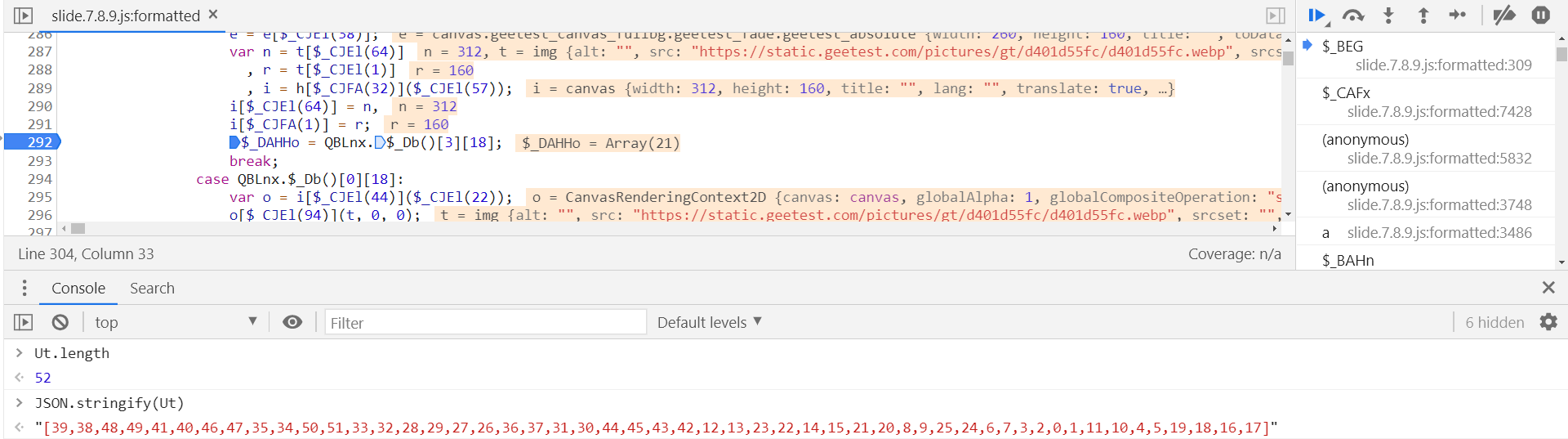
[39,38,48,49,41,40,46,47,35,34,50,51,33,32,28,29,27,26,36,37,31,30,44,45,43,42,12,13,23,22,14,15,21,20,8,9,25,24,6,7,3,2,0,1,11,10,4,5,19,18,16,17]
示例:

Python 复现:
def restore_picture():
img_list = ["./乱序缺口背景图.png", "./乱序背景图.png"]
for index, img in enumerate(img_list):
image = Image.open(img)
s = Image.new("RGBA", (260, 160))
ut = [39, 38, 48, 49, 41, 40, 46, 47, 35, 34, 50, 51, 33, 32, 28, 29, 27, 26, 36, 37, 31, 30, 44, 45, 43,42,12, 13, 23, 22, 14, 15, 21, 20, 8, 9, 25, 24, 6, 7, 3, 2, 0, 1, 11, 10, 4, 5, 19, 18, 16, 17]
height_half = 80
for inx in range(52):
c = ut[inx] % 26 * 12 + 1
u = height_half if ut[inx] > 25 else 0
l_ = image.crop(box=(c, u, c + 10, u + 80))
s.paste(l_, box=(inx % 26 * 10, 80 if inx > 25 else 0))
if index == 0:
s.save("./缺口背景图片.png")
else:
s.save("./背景图片.png")
还原后如下:

错误结果
// challenge 不对
geetest_xxxxxxxxxxxxx({"status": "error", "error": "illegal challenge", "user_error": "\u7f51\u7edc\u4e0d\u7ed9\u529b", "error_code": "error_23"})
// w 不对
geetest_xxxxxxxxxxxxx({"status": "error", "error": "param decrypt error", "user_error": "\u7f51\u7edc\u4e0d\u7ed9\u529b", "error_code": "error_03"})
// 无轨迹
geetest_xxxxxxxxxxxxx({"status": "error", "error": "not proof", "user_error": "\u7f51\u7edc\u4e0d\u7ed9\u529b", "error_code": "error_21"})
// 轨迹、缺口距离、参数问题
geetest_xxxxxxxxxxxxx({"success": 0, "message": "fail"})
geetest_xxxxxxxxxxxxx({"success": 0, "message": "forbidden"})
结果验证
100 次大概 95% 的成功率: